Уравнение маятника
Рассмотрим движения хорошо известного математического маятника, т. е. небольшого грузика с массой m, подвешенного на абсолютно жесткой, нерастяжимой проволочке длины l; массу проволочки будем считать пренебрежимо малой. Обычно изучают малые колебания и поэтому говорят о грузике на нитке, но мы хотим изучать любые движения и потому подвесим наш жесткий маятник на хорошо смазанной оси в точке О' так, чтобы он мог свободно вращаться, а не только качаться вблизи положения равновесия. Угол ?, измеряемый в радианах, отсчитывается от нижнего положения против часовой стрелки (рис. 4.1). Полный оборот соответствует ? = 2?, два оборота — 4? и т. д. Движению по часовой стрелке соответствует уменьшение угла ?. для полного оборота по часовой стрелке ? = -2? и т. д. Для определенности будем считать, что в момент времени t = 0 маятник отклонен на нулевой угол, ?(0) = 0. В качестве координаты грузика можно взять угол ? или же алгебраическое значение длины дуги s = ? • l.
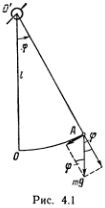
В каждой точке А движение происходит в направлении касательной к окружности под действием тангенциальной (направленной по касательной) составляющей силы тяжести. Как ясно из рисунка, эта составляющая равна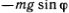 
(с учетом нашего выбора положительного направления движения). Скорость движения грузика по окружности равна v = s' = l?', где s' и ?' обозначают производные по времени t. Пользуясь тем, что малые смещения грузика направлены по касательной к окружности, точно так же определим тангенциальное (т. е. по направлению дуги окружности) ускорение а = v' == s" = l?", где s" и ?" — вторые производные по времени. Второй закон Ньютона для движения грузика можно написать в виде ma = 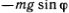, или окончательно
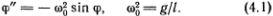
Соотношение (4.1), выражающее угловое ускорение грузика ?" через его положение ?(t) в тот же самый момент времени, называют дифференциальным уравнением движения грузика. Решить его значит найти такую зависимость угла ? от времени t, для которой в каждый момент выполнено соотношение (4.1).
Дифференциальное уравнение описывает все возможные движения маятника. Чтобы найти какое-то конкретное движение, надо еще добавить некоторые дополнительные условия. Например, если задать положение и скорость грузика в начальный момент времени, то движение будет полностью определено. Как сказал бы математик, существует единственное решение дифференциального уравнения (4.1), удовлетворяющее начальным условиям ?(0) = ?0, ?'(0) = ?'0, (?0 и ?'0 могут быть любыми).
Это уравнение, очевидно, нелинейно. Даже если известны какие-то два его решения ?1(t) и ?2(t), новое решение их сложением не получишь. Ясно также, что умножение решения на число с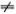 
1 не дает нового решения: вторая производная от с?1 равна с?"1, а 
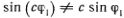. Правда, есть простой случай, когда ?1 + ?2 тоже есть решение, но, к сожалению, этот случай не интересен, так как дает просто разное описание состояния покоящегося маятника. Действительно, уравнение имеет простые решения ? = 
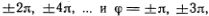... Первая серия соответствует устойчивому положению равновесия маятника внизу (минимум потенциальной энергии). Грузик покоится, его скорость, ускорение и действующая на него сила равны нулю. А вторая серия — это неустойчивое положение равновесия в крайней верхней точке (максимум потенциальной энергии). Если грузик чуть-чуть отклонится от этого положения, то он придет в движение. Так как в реальном физическом мире всегда остаются какие-то малые неконтролируемые воздействия на грузик («возмущения»), долго находиться в этом состоянии он не может.