§ 7. Изменение средних со временем

Теперь мы познакомим вас с еще одной интересной вещью: вы узнаете, как средние изменяются во времени. Представим на минуту, что у нас есть оператор ^A, в который время явным образом не входит. Имеется в виду такой оператор, как ^x или ^p. [А исключаются, скажем, такие вещи, как оператор внешнего потенциала V(x, t), меняющийся во времени.] Теперь представим, что мы вычислили <A>_ср в некотором состоянии |?>, т. е.

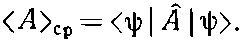(18.76)

Как <A>_ср будет зависеть от времени? Но почему оно вообще может зависеть от времени? Ну, во-первых, может случиться, что оператор сам явно зависит от времени, например, если он был связан с переменным потенциалом типа V(x, t). Но даже если оператор от t не зависит, например оператор ^A=^x, то соответствующее среднее может зависеть от времени. Ведь среднее положение частицы может перемещаться. Но как может такое движение получиться из (18.76), если А от времени не зависит? Дело в том, что во времени может меняться само состояние |?>. Для нестационарных состояний мы часто даже явно отмечали зависимость от времени, записывая их как |?(t)>. Теперь мы хотим показать, что скорость изменения <A>_ср дается новым оператором, который мы обозначим ^A. Напомним, что ^A это оператор, так что точка над А вовсе не означает дифференцирования по времени, а является просто способом записи нового оператора ^A, определяемого равенством

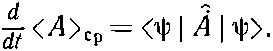(18.77)

Задачей нашей будет найти оператор ^^.A.

Прежде всего, нам известно, что скорость изменения состояния дается гамильтонианом. В частности,

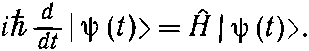(18.78)

Это всего-навсего абстрактная форма записи нашего первоначального определения гамильтониана

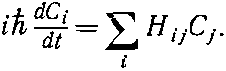(18.79)

Если мы комплексно сопряжем это уравнение, оно будет эквивалентно

(18.80)

Посмотрим теперь, что случится, если мы продифференцируем (18.76) по t. Поскольку каждое ? зависит от t, мы имеем

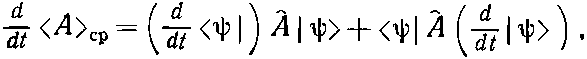(18.81)

Наконец, заменяя производные их выражениями (18.78) и (18.80), получаем

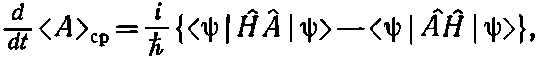
а это то же самое, что написать

Сравнивая это уравнение с (18.77), мы видим, что

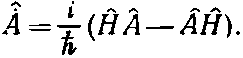(18.82)

Это и есть то интересное соотношение, которое мы обещали; и оно справедливо для любого оператора А.

Кстати заметим, что, если бы оператор А сам зависел от времени, мы бы получили

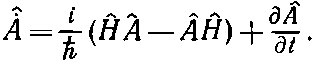(18.83)

Проверим (18.82) на каком-либо примере, чтобы посмотреть, имеет ли оно вообще смысл. Какой, например, оператор соответствует х? Мы утверждаем, что это должно быть

(18.84)

Что это такое? Один способ установить, что это такое — перейти в координатное представление и воспользоваться алгебраическим оператором ^?. В этом представлении коммутатор равен

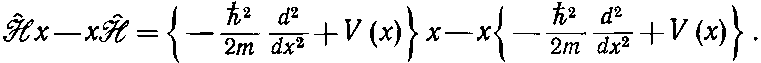
Если вы подействуете всем этим выражением на волновую функцию ?(х) и вычислите везде, где нужно, производные, вы в конце концов получите

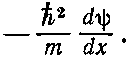
Но это то же самое, что и

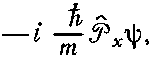
так что мы обнаруживаем, что

(18.85)

или что

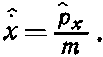(18.86)

Прелестный результат. Он означает, что если среднее значение х меняется со временем, то перемещение центра тяжести равно среднему импульсу, деленному на массу m. Точно как в классической механике.

Другой пример. Какова скорость изменения среднего импульса состояния? Правила игры прежние. Оператор этой скорости равен

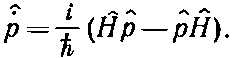(18.87)

Опять все можно подсчитать в x-представлении. Напомним, что ^p обращается в d/dx, а это означает, что вам придется дифференцировать потенциальную энергию V (в ^?), но только во втором слагаемом. В конце концов остается только один член, и вы получаете

или

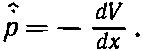(18.88)

Опять классический результат. Справа стоит сила, так что мы вывели закон Ньютона! Но помните — это законы для операторов, которые дают средние величины. Они не описывают в деталях, что происходит внутри атома.

Существенное отличие квантовой механики в том, что ^p^x не равно ^x^p. Они отличаются на самую малость — на маленькое число ?. Но все поразительные сложности интерференции волн и тому подобного проистекают из того небольшого факта, что ^x^p-^p^x не совсем нуль.

История этой идеи тоже интересна. С разницей в несколько месяцев в 1926 г. Гейзенберг и Шредингер независимо отыскали правильные законы, описывающие атомную механику. Шредингер изобрел свою волновую функцию ?(х) и нашел уравнение для нее, а Гейзенберг обнаружил, что природу можно было бы описывать и классическими уравнениями, лишь бы хр-рх было равно ?/i, чего можно было добиться, определив их с помощью особого вида матриц. На нашем теперешнем языке он пользовался энергетическим представлением и его матрицами. И то и другое — и матричная алгебра Гейзенберга и дифференциальное уравнение Шредингера — объясняли атом водорода. Несколькими месяцами позднее Шредингер смог показать, что обе теории эквивалентны — мы только что это видели. Но две разные математические формы квантовой механики были открыты независимо.