§ 3. Решение уравнений для двух состояний

Теперь можно писать наше уравнение двух состояний в различных видах, например:

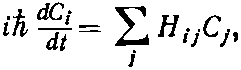
или вот так:

(9.30)

Оба они означают одно и то же. Для частицы со спином ¹/₂ в магнитном поле гамильтониан Н дается уравнением (9.8) или (9.13).

Если поле направлено по z, то, как мы уже много раз видели, решение заключается в том, что состояние |?>, каким бы оно ни было, прецессирует вокруг оси z (в точности, как если бы взять физическое тело и вращать его как целое вокруг оси z) с угловой скоростью, вдвое большей, чем ?B/?. Все это, конечно, относится и к магнитному полю, направленному под другим углом, ведь физика от системы координат не зависит. Если магнитное поле время от времени как-то сложно меняется, то такое положение вещей можно анализировать следующим образом. Пусть вначале спин был в направлении +z, а магнитное поле — в направлении х. Спин начал поворачиваться. Если выключить x-поле, поворот прекратится. Если теперь включить z-поле, спин начнет поворачиваться вокруг z и т. д. Значит, смотря по тому, как меняются поля во времени, вы можете представить себе, каким будет конечное состояние — по какой оси оно будет направлено. Затем можно отнести это состояние к первоначальным |+> и |-> по отношению к z, пользуясь проекционными формулами, полученными в гл. 8 (или в гл. 4). Если в конечном состоянии спин направлен по (?, ?), то амплитуда того, что спин будет смотреть вверх, равна cos(?/2)e^-i?/2, а амплитуда того, что спин будет смотреть вниз, равна sin(?/2)e^+i?/2. Это решает любую задачу. Таково словесное описание решений дифференциальных уравнений.

Только что описанное решение достаточно общо для того, чтобы справиться с любой системой с двумя состояниями. Возьмем наш пример с молекулой аммиака, на которую действует электрическое поле. Если система описывается на языке состояний |I> и |II>, то уравнения выглядят так:

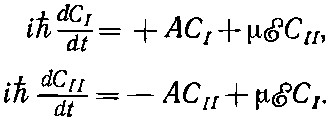(9.31)

Вы скажете: «Нет, там, я помню, стояло еще E₀». Неважно, мы просто сдвинули начало отсчета энергий, чтобы Е₀ стало равно нулю. (Это всегда можно сделать, изменив обе амплитуды в одно и то же число раз — в exp(iE₀T/?); так можно избавиться от любой постоянной добавки к энергии.) Одинаковые уравнения обладают одинаковыми решениями, поэтому не стоит решать их вторично. Если взглянуть на эти уравнения и на (9.1), то их можно отождествить между собой следующим образом. Состояние |+> обозначим |I>, состояние |-> обозначим |II>. Это вовсе не значит, что мы выстраиваем аммиак в пространстве в одну линию или что |+> и |-> как-то связаны с осью z. Это все делается чисто искусственно. Имеется искусственное пространство, которое можно было бы назвать, например, «модельным пространством молекулы аммиака» или еще как-нибудь иначе. Это просто трехмерная «диаграмма», и направление «вверх» означает пребывание молекулы в состоянии |I>, а направление «вниз» по фальшивой оси z означает пребывание молекулы в состоянии |II>. Тогда уравнения отождествляются следующим образом.

Прежде всего вы видите, что гамильтониан может быть записан через матрицы сигма:

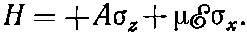(9.32)

Если сравнить это с (9.1), то ?B_z будет соответствовать -А, а ?В_х будет соответствовать -??. В нашем «модельном» пространстве возникает, стало быть, постоянное поле В, направленное по оси z. Если есть, кроме этого, электрическое поле ?, меняющееся со временем, то у поля В появится и пропорционально меняющаяся x-компонента. Таким образом, поведение электрона в магнитном поле с постоянной составляющей в направлении z и колеблющейся составляющей в направлении х математически во всем подобно и точно соответствует поведению молекулы аммиака в осциллирующем электрическом поле. К сожалению, у нас нет времени входить глубже в детали этого соответствия или разбираться в каких-либо технических деталях. Мы только хотели подчеркнуть, что можно сделать так, чтобы все системы с двумя состояниями были аналогичны объекту со спином ¹/₂, прецессирующему в магнитном поле.