§ 5. Распад Λ0

Теперь приведем пример того, как теорема о сохранении момента количества движения применяется в чисто квантовофизических задачах. Рассмотрим распад лямбда-частицы (?⁰), которая расщепляется на протон и ?^--мезон посредством слабого взаимодействия:

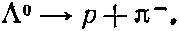
Пусть нам известно, что спин у пиона равен нулю, у протона — половине, а у ?⁰ тоже половине. Мы хотели бы решить следующую задачу: положим, что ?⁰ рождена таким образом, что оказалась полностью поляризованной; это значит, что ее спин направлен, скажем, вверх по отношению к подходящим образом выбранной оси z (фиг. 15.6, а).

Фиг. 15.6. ?⁰-частица со спином, направленным вверх, распадается на протон и пион (в системе центра масс). Какова вероятность того, что протон вылетит под углом ??

Вопрос заключается в том, с какой вероятностью она распадется так, что протон вылетит под углом ? к оси z (фиг. 15.6, б). Иными словами, каково угловое распределение распадов? Мы будем рассматривать распад в системе координат, где ?⁰ покоится, измеряя углы в системе покоя ?⁰; если нужно, их всегда можно перевести в другую систему.

Начнем с рассмотрения того частного случая, когда протон испускается в небольшой телесный угол ?? близ оси z (фиг. 15.7).

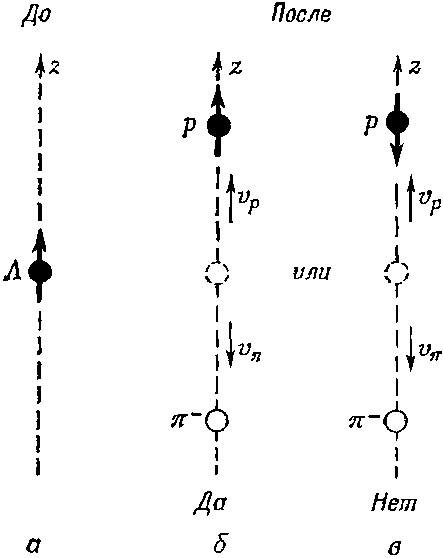
Фиг. 15.7. Две возможности распада частицы ?⁰ со спином, направленным вверх, если протон движется по оси +z. Момент сохраняется только при схеме распада (б).

До распада спин ?⁰ был направлен вверх (фиг. 15.7, а). Через мгновение (по причинам, по сей день неизвестным, известно только, что они связаны со слабыми распадами) ?⁰ взрывается, образуя протон и пион. Пусть протон летит вверх по оси +z. Тогда пиону из-за сохранения импульса придется направиться вниз. Поскольку протон — это частица со спином ¹/₂, то его спин обязан быть направлен либо вверх, либо вниз,— в принципе имеются две возможности, показанные на фиг. 15.7, б и в. Сохранение момента количества движения требует, однако, чтобы спин протона был направлен только вверх. Легче всего понять это из следующих рассуждений. Частица, движущаяся вдоль оси z, никак не может приобрести за счет своего движения момента вокруг этой оси, поэтому в J_z могут дать вклад только спины. Спиновый момент количества движения вокруг оси z до распада был равен +?/2; значит, и после он будет равен +?/2. Можно сказать, что из-за того, что у пиона нет спина, спин протона должен смотреть вверх.

Если вас тревожит, что такого рода рассуждения могут в квантовой механике оказаться неправильными, стоит потратить минутку, чтобы показать, что и по квантовой механике все обстоит так же. Начальное (дораспадное) состояние, которое мы обозначим |?⁰, спин по +z>, обладает тем свойством, что если его повернуть вокруг оси z на угол ?, то вектор состояния умножается на фазовый множитель e^i?/2. (В повернутой системе вектор состояния равен e^itf/2|?⁰, спин но +z>.) Именно это и имеют в виду, говоря о спине вверх у частицы со спином ¹/₂. Поскольку поведение природы не зависит от нашего выбора осей, то конечное состояние системы «протон плюс пион» должно обладать тем же свойством. Конечное состояние мы можем, например, записать в виде

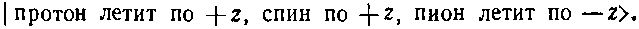
Но движение пиона на самом деле не нужно оговаривать, потому что в выбранной нами системе пион всегда движется противоположно протону; наше описание конечного состояния можно упростить до

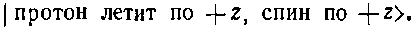
Так что же случится с этим состоянием, если мы повернем систему координат вокруг оси z на угол ??

Раз протон и пион движутся вдоль оси z, их движение поворотом не изменишь. (Вот почему мы и выбрали этот частный случай; иначе бы наше рассуждение не прошло.) Значит, с пионом ничего не случится, потому что спин его равен нулю. У протона, однако, спин равен ¹/₂. Если его спин направлен вверх, он в ответ на поворот изменит фазовый множитель в e^i?/2 раз. (А если бы спин его был направлен вниз, то изменение фазы стало бы e^-i?/2.) Но если момент количества движения обязан сохраняться (а это так, ибо в гамильтониане нет факторов, зависящих от внешних воздействий), то изменение фазы из-за поворота должно быть до распада и после распада одно и то же. Итак, единственная возможность состоит в том, что спин протона будет направлен вверх. Если протон двинулся вверх, то и спин его должен быть направлен вверх.

Мы, следовательно, заключаем, что сохранение момента количества движения разрешает процесс, показанный на фиг. 15.7, б, но не разрешает процесса, показанного на фиг. 15.7, в. А раз мы знаем, что распад все же происходит, то, значит, имеется некоторая амплитуда для процесса, показанного на фиг. 15.7, б, когда протон летит вверх и спин его при этом тоже смотрит вверх. И мы обозначим буквой а амплитуду того, что в бесконечно малый промежуток времени произойдет такой распад[67].

Теперь посмотрим, что было бы, если бы спин ?⁰ вначале был направлен вниз. Опять рассматриваем распады, в которых протон взлетает вверх по оси z, как показано на фиг. 15.8.

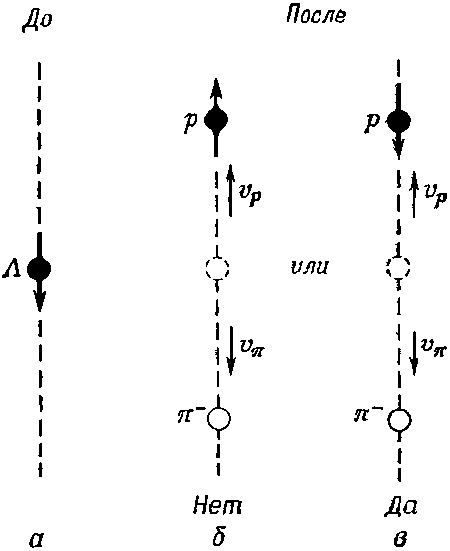
Фиг. 15.8. Распад вдоль оси z для ?⁰ со спином, направленным вниз.

Вам, конечно, теперь ясно, что в этом случае спин протона направлен вниз (если только момент количества движения сохраняется). Обозначим амплитуду такого распада буквой b.

Об амплитудах а и b мы ничего больше сказать не сможем. Они зависят от внутренней механики частицы ?⁰ и от слабых распадов, и никто пока не знает, как их подсчитывать. Их приходится получать из опыта. Но, зная только эти две амплитуды, мы можем узнать об угловом распределении распадов все, что захотим. Надо только всегда тщательно и полностью определять те состояния, о которых идет речь.

Мы хотим знать вероятность того, что протон вылетит под углом ? к оси z (в некоторый узкий телесный угол ??), как показано на фиг. 15.6. Проведем новую ось z в этом направлении и обозначим ее z'! Как анализировать, что происходит вдоль этой оси, мы знаем. По отношению к ней спин ?⁰ уже не направлен вверх, а имеет какую-то амплитуду того, что он окажется направленным вверх и какую-то — вниз. Все это мы уже подсчитывали в гл. 4, а потом опять в гл. 8 [уравнение (8.30)] (вып. 8). Амплитуда того, что спин будет направлен вверх, есть cos?/2, а амплитуда того, что спин будет смотреть вниз, есть -sin?/2[68]. Когда спин ?⁰ направлен вверх по оси z', она испустит протон в направлении z с амплитудой а. Значит, амплитуда того, что по направлению z пройдет протон, держа свой спин вверх, равна

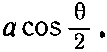(15.33)

Точно так же амплитуда того, что вдоль положительной оси z пройдет протон, направив свой спин вниз, равна

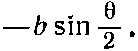(15.34)

Те два процесса, к которым относятся эти амплитуды, показаны на фиг. 15.9.

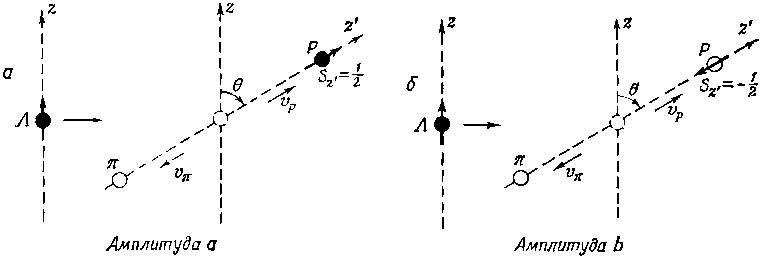
Фиг. 15.9. Два возможных состояния распада ?⁰.

Теперь зададим такой немудреный вопрос. Пусть мы собираемся регистрировать протоны, вылетающие под углом ?, не интересуясь их спином. Два спиновых состояния (вверх и вниз по оси z') различимы, даже если бы мы того и не хотели. Значит, чтобы получить вероятность, надо амплитуды возвысить в квадрат и сложить. Вероятность f(?) обнаружить протон в небольшом телесном угле ?? при ? равна

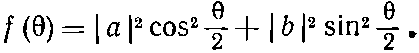(15.35)

Вспоминая, что sin²?/2=¹/₂(1-cos?) и cos²?/2=¹/₂(1+cos?), запишем f(?) так:

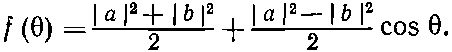(15.36)

Угловое распределение имеет вид

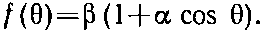(15.37)

Одна часть вероятности не зависит от ?, а другая зависит от cos? линейно. Из измерений углового распределения мы можем получить ? и ?, а значит, и |а|, и |b|.

Можно получить ответ и на многие другие вопросы. Может быть, вас интересуют лишь те протоны, спин которых направлен вверх относительно старой оси z? Каждый член в (15.33) и (15.34) даст амплитуду того, что спин протона окажется направленным вверх или вниз по отношению к оси z'(|+z'> и |-z'>). А состояние, когда спин направлен вверх относительно старой оси, |+z>, можно выразить через два базисных состояния |+z'> и |-z'>. Можно тогда взять две амплитуды (15.33) и (15.34) с надлежащими коэффициентами (cos?/2 и -sin?/2) и получить полную амплитуду

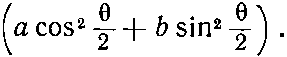
Ее квадрат даст вероятность того, что протон вылетит под углом ? со спином, направленным туда же, куда направлен спин ?⁰ (вверх по оси z).

Если бы четность сохранялась, можно было бы сделать еще одно утверждение. Распад на фиг. 15.8 — это просто зеркальное отражение, скажем в плоскости yz, распада с фиг. 15.7[69]. Если бы четность сохранялась, b равнялось бы либо a, либо -а. Тогда коэффициента в (15.37) был бы равен нулю и распад одинаково часто происходил бы во всех направлениях.

Результаты опытов говорят, однако, что при распаде асимметрия существует. Измеренное угловое распределение действительно, как мы предсказали, меняется по закону cos?, а не по закону cos²? или по другой степени. Из этого углового распределения, стало быть, следует, что спин ?⁰ равен ¹/₂. Кроме того, мы видим, что четность не сохраняется. Действительно, коэффициент a на опыте найден равным -0,62±0,05, так что b примерно вдвое больше а. Отсутствие симметрии относительно отражений совершенно очевидно.

Вы видите, как много можно вывести из сохранения момента количества движения. Еще некоторые примеры будут приведены в следующей главе.

* * *

Замечание после лекции. Под амплитудой а здесь мы подразумевали амплитуду того, что состояние |протон летит по +z, спин по +z> образовано за бесконечно малое время dt из состояния |?, спин по +z>, или, иными словами, что

(15.38)

где H — гамильтониан всего мира или по крайней мере той его части, которая ответственна за ?-распад. Сохранение момента количества движения означает, что у гамильтониана должно быть такое свойство:

(15.39)

Под амплитудой b подразумевается, что

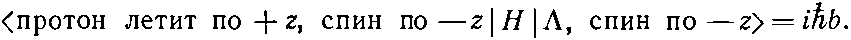(15.40)

Сохранение момента количества движения предполагает, что

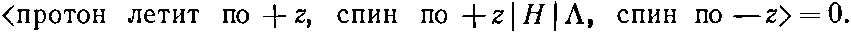(15.41)

Если вам не ясно, как написаны амплитуды (15.33) и (15.34), можно их записать в более математической форме. Когда мы писали (15.33), нам нужна была амплитуда того, что ? со спином, направленным по +z, распадается на протон, движущийся вдоль направления +z' и обладающий спином, направленным тоже по +z', т. е.

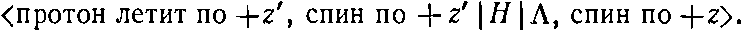(15.42)

По общим теоремам квантовой механики эту амплитуду можно записать так:

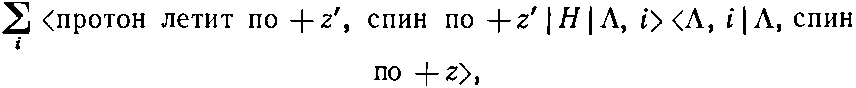(15.43)

где суммирование проводится но базисным состояниям |?, i> покоящейся ?-частицы. Поскольку спин ?-частицы равен ¹/₂, таких состояний два, в каком бы базисе мы ни работали. Если в качестве базисных мы выберем состояния со спином, направленным вверх и вниз по отношению к оси z'(|+z'>, |-z'>), то амплитуда (15.43) будет равна сумме

(15.44).

Первый множитель в первом слагаемом равен а [из (15.38)], а первый множитель во втором слагаемом равен нулю — из формулы (15.41), в свою очередь следующей из сохранения момента количества движения. Второй множитель <?, +z'|?, +z> из первого слагаемого — это как раз амплитуда того, что частица со спином ¹/₂, направленным вверх по одной оси, будет также обладать спином, направленным вверх по другой оси, повернутой относительно первой на угол ?. Такая амплитуда равна cos?/2 [см. табл. 4.2 (вып. 8)]. Так что (15.44) равно просто а cos?/2, как и было написано в (15.33). Амплитуда (15.34) следует из таких же рассуждений для ?-частицы со спином, направленным вниз.

* * *