§ 6. Момент количества движения

Для интереса рассмотрим еще одну операцию — операцию орбитального момента количества движения. В гл. 15 мы определили оператор ^J_z через ^R_z(?) — оператор поворота на угол ? вокруг оси z. Рассмотрим сейчас систему, описываемую всего лишь одной-единственной волновой функцией ?(r), которая является функцией одних только координат и не учитывает того факта, что спин у электрона должен быть направлен либо вверх, либо вниз. Это значит, что мы собираемся пока пренебречь внутренним моментом количества движения и намерены думать только об орбитальной части. Чтобы подчеркнуть различие, обозначим орбитальный оператор ^L_z и определим его через оператор поворота на бесконечно малый угол ? формулой

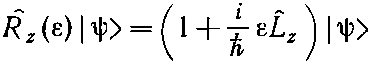
(напоминаем: это определение применимо только к состоянию |?>, у которого нет внутренних спиновых переменных, а есть только зависимость от координат r: х, у, z). Если мы взглянем на состояние |?> из новой системы координат, повернутой вокруг оси z на небольшой угол ?, то увидим новое состояние:

Если мы решили описывать состояние |?> в координатном представлении, т. е. с помощью его волновой функции ?(r), то следует ожидать такого равенства:

(18.68)

Что же такое ^?? А вот что. Точка Р(х, у) в новой системе координат (на самом деле х', у', но мы убрали штрихи) раньше имела координаты x-?y и y+?x (фиг. 18.2).

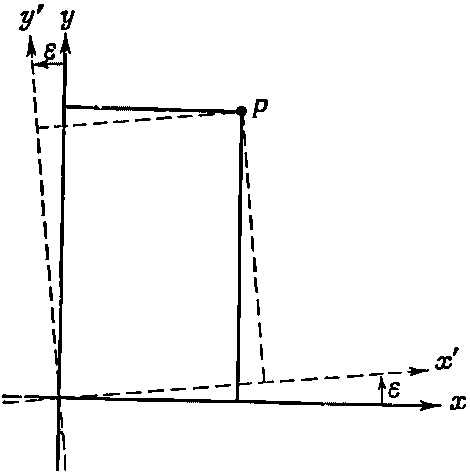
Фиг. 18.2. Поворот осей вокруг оси z на малый угол ?.

Поскольку амплитуда того, что электрон окажется в точке Р, не меняется от поворота системы координат, то можно писать

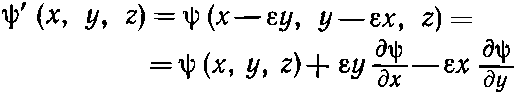
(напоминаем, что ? — малый угол). Это означает, что

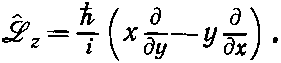(18.69)

Это и есть наш ответ. Обратите, однако, внимание, что это определение эквивалентно такому:

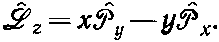(18.70)

Или, если вернуться к нашим квантовомеханическим операторам, можно написать

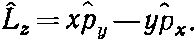(18.71)

Эту формулу легко запомнить, потому что она похожа на знакомую формулу классической механики: это z-компонента векторного произведения

(18.72)

Одна из забавных сторон манипуляций с операторами заключается в том, что многие классические уравнения переносятся в квантовомеханическую форму. А какие нет? Ведь должны же быть такие, которые не получаются, потому что если бы все повторялось, то в квантовой механике не было бы ничего отличного от классической, не было бы новой физики.

Вот вам уравнение, которое отличается. В классической физике

А что в квантовой механике?

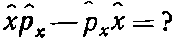
Подсчитаем это в x-представлении. Чтобы было видно, что мы делаем, приложим это к некоторой волновой функции ?(x). Пишем

или

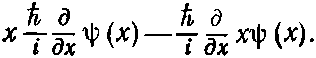
Вспомним теперь, что производные действуют на всё, что справа. Получаем

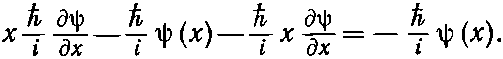(18.73)

Ответ не нуль. Вся операция попросту равнозначна умножению на -?/i:

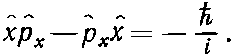(18.74)

Если бы постоянная Планка была равна нулю, то квантовые и классические результаты стали бы одинаковыми и не пришлось бы нам учить никакой квантовой механики!

Отметим, что если два каких-то оператора А и В, взятые в сочетании

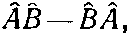
не дают нуля, то мы говорим, что «операторы не перестановочны», или «операторы не коммутируют». А уравнение наподобие (18.74) называется «перестановочным соотношением». Вы можете сами убедиться, что перестановочное соотношение для p_х и у (или коммутатор р_х и у) имеет вид

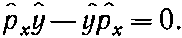
Существует еще одно очень важное перестановочное соотношение. Оно относится к моментам количества движения. Вид его таков:

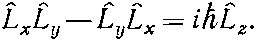(18.75)

Если вы хотите приобрести некоторый опыт работы с операторами ^x и ^p, попробуйте доказать эту формулу сами.

Интересно заметить, что операторы, которые не коммутируют, можно встретить и в классической физике. Мы с этим уже сталкивались, когда говорили о поворотах в пространстве. Если вы повернете что-нибудь, например книжку, сперва на 90° вокруг оси х, а затем на 90° вокруг оси у, то получится совсем не то, что было бы, если бы сначала вы повернули ее на 90° вокруг оси у, а после на 90° вокруг оси х. Именно это свойство пространства и ответственно за уравнение (18.75).