§ 5. Измерение ядерного спина

Продемонстрируем теперь пример, где понадобятся только что описанные коэффициенты. Он связан с проделанными не так давно интересными опытами, которые вы теперь в состоянии будете понять. Некоторым физикам захотелось узнать спин одного из возбужденных состояний ядра Ne²⁰. Для этого они принялись бомбить углеродную мишень пучком ускоренных ионов углерода и породили нужное им возбужденное состояние Ne²⁰ (обозначаемое Ne^20*) в реакции

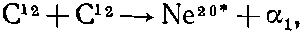
где ?₁ — это ?-частица, или Не⁴. Кое-какие из создаваемых таким образом возбужденных состояний Ne²⁰ неустойчивы и распадаются таким путем:

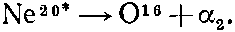
Значит, на опыте видны возникающие в реакции две ?-частицы. Обозначим их ?₁ и ?₂; поскольку они вылетают с разными энергиями, их можно отличить друг от друга. Кроме того, выбирая ?₁, имеющие нужную энергию, мы можем отобрать любые возбужденные состояния Ne²⁰.

Опыт ставился так, как показано на фиг. 16.9.

Фиг. 16.9. Размещение приборов в опыте по определению спина возбужденных состояний Ne²⁰.

Пучок ионов углерода с энергией 16 Мэв был направлен на углеродную пленку. Первая ?-частица регистрировалась кремниевым детектором, настроенным на прием ?-частиц с нужной энергией, движущихся вперед (по отношению к падающему пучку ионов С¹²). Вторая ?-частица регистрировалась счетчиком ?₂, поставленным под углом ? к ?₁. Скорость счета сигналов совпадений от ?₁ и ?₂ измерялась как функция угла ?.

Идея опыта в следующем. Прежде всего нужно знать, что спины С¹², О¹⁶ и ?-частицы все равны нулю. Назовем направление движения начальных частиц С¹² направлением +z; тогда известно, что Ne^20* должен обладать нулевым моментом количества движения относительно оси z. Ведь ни у одной из остальных частиц нет спина; кроме того, С¹² прилетает вдоль оси z и ?₁ улетает вдоль оси z, так что у них не может быть момента относительно этой оси. И каким бы ни был спин j ядра Ne^20*, мы знаем, что это ядро находится в состоянии |j, 0>. Что же случится, когда Ne^20* распадется на О¹⁶ и другую ?-частицу? Что ж, ?-частицу поймает счетчик ?₂, а О¹⁶, чтобы сохранить начальный импульс, вынужден будет уйти в противоположную сторону[76]. Относительно новой оси (оси ?₂) не может быть тоже никакой компоненты момента количества движения. А раз конечное состояние имеет относительно новой оси нулевой момент количества движения, то у распада Ne^20* должна быть некоторая амплитуда того, что m'=0, где m'—квантовое число компоненты момента количества движения относительно новой оси. Вероятность наблюдать ?₂ под углом ? будет на самом деле равна квадрату амплитуды (или матричного элемента)

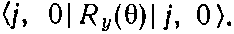(16.41)

Чтобы получить спин интересующего нас состояния Ne^20*, вычертим интенсивность наблюдений второй ?-частицы как функцию угла и сравним с теоретическими кривыми для различных значений j. Как мы отмечали в конце предыдущего параграфа, амплитуды <j,0|R_y(?)|j,0>—это просто функции Р_j(cos?). Значит, угловые распределения будут следовать кривым [P_j(cos?)]². Экспериментальные результаты для двух возбужденных состояний показаны на фиг. 16.10.

Фиг. 16.10. Экспериментальные результаты измерений углового распределения ?-частиц, вылетающих при распаде двух возбужденных состояний Ne²⁰. Они получены на устройстве, показанном на фиг. 16.9.

Вы видите, что угловое распределение для состояния 5,80 Мэв очень хорошо укладывается на кривую [Р₁(cos?)]², т. е. оно должно быть состоянием со спином 1. С другой стороны, данные для состояния 5,63 Мэв выглядят совершенно иначе; они ложатся на кривую [Р₃(cos?)]². Спин этого состояния равен 3.

В этом опыте мы измерили момент количества движения двух возбужденных состояний Ne^20*. Этой информацией можно воспользоваться, чтобы понять, как ведут себя протоны и нейтроны внутри этого ядра, и это принесет нам добавочные сведения о таинственных ядерных силах.