§ 3. Уровни энергии

We use cookies. Read the Privacy and Cookie Policy

Теперь мы готовы к тому, чтобы вычислить уровни энергии основного состояния водорода, решая гамильтоновы уравнения (10.14). Мы хотим найти энергии стационарных состояний. Это значит, что мы должны отыскать те особые состояния |?>, для которых каждая из принадлежащих |?> амплитуд Ci=<i|?> обладает одной и той же зависимостью от времени, а именно е-?t. Тогда состояние будет обладать энергией E=??. Значит, мы ищем совокупность амплитуд, для которых

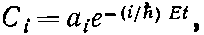(10.17)

где четверка коэффициентов аi не зависит от времени. Чтобы увидеть, можем ли мы получить эти амплитуды, подставим (10.17) в (10.14) и посмотрим, что из этого выйдет. Каждое i?dCi/dt в (10.14) перейдет в ECi. И после сокращения на общий экспоненциальный множитель каждое Сi превратится в аi; получим

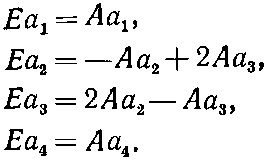(10.18)

Это и нужно решить для отыскания a1, а2, а3и а4. Право, очень мило со стороны первого уравнения, что оно не зависит от остальных, — а это значит, что одно решение сразу видно. Если выбрать Е=А, то

даст решение. (Конечно, если принять все а равными нулю, то это тоже будет решение, но состояния оно не даст!) Будем считать наше первое решение состоянием[41] |I>:

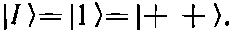(10.19)

Его энергия

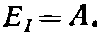
Все это немедленно дает ключ ко второму решению, получаемому из последнего уравнения в (10.18):

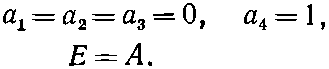
Это решение мы назовем состоянием |II>:

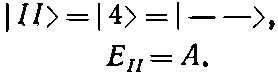(10.20)

Дальше пойдет чуть труднее; оставшиеся два уравнения (10.18) переплетены одно с другим. Но мы все это уже делали. Сложив их, получим

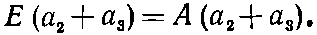(10.21)

Вычитая, будем иметь

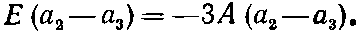(10.22)

Окидывая это взглядом и припоминая знакомый нам уже аммиак, мы видим, что здесь есть два решения:

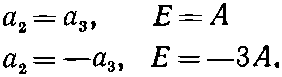(10.23)

Это смеси состояний |2> и |3>. Обозначая их |III> и |IV> и вставляя для правильной нормировки множитель 1/?2, имеем

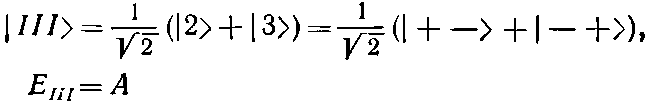(10.24)

и

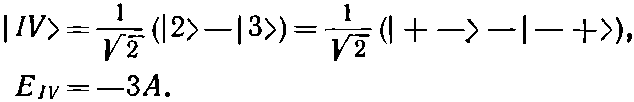(10.25)

Мы нашли четверку стационарных состояний и их энергии. Заметьте, кстати, что наши четыре состояния ортогональны друг другу, так что их тоже можно при желании считать базисными состояниями. Задача наша полностью решена.

У трех состояний энергия равна А, а у последнего -3А. Среднее равно нулю, а это означает, что когда в (10.5) мы выбрали Е0=0, то тем самым мы решили отсчитывать все энергии от их среднего значения. Диаграмма уровней энергии основного состояния водорода будет выглядеть так, как на фиг. 10.2.

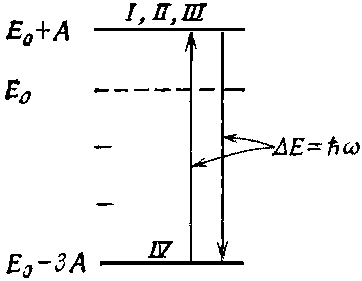
Фиг. 10.2. Диаграмма уровней энергии основного состояния атомарного водорода.

Различие в энергиях между состоянием |IV> и любым из остальных равно 4A. Атом, который случайно окажется в состояний |I>, может оттуда упасть в состояние |IV> и испустить свет: не оптический свет, потому что энергия очень мала, а микроволновой квант. Или, если осветить водородный газ микроволнами, мы заметим поглощение энергии, оттого что атомы в состоянии |IV> будут ее перехватывать и переходить в одно из высших состояний, но все это только на частоте ?=4A/?. Эта частота была измерена экспериментально; наилучший результат, полученный сравнительно недавно[42], таков:

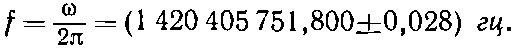(10.26)

Ошибка составляет только три стомиллиардных! Вероятно, ни одна из фундаментальных физических величин не измерена лучше, чем эта; таково одно из наиболее выдающихся по точности измерений в физике. Теоретики были очень счастливы, когда им удалось вычислить энергию с точностью до 3·10-5; но к этому времени она была измерена с точностью до 2·10-11,т.е. в миллион раз точнее, чем в теории. Так что экспериментаторы идут далеко впереди теоретиков. В теории основного состояния атома водорода и вы, и мы находимся в одинаковом положении. Вы ведь тоже можете взять значение А из опыта — и всякому, в конце концов, приходится делать то же самое.

Вы, вероятно, уже слышали раньше о «21-см линии» водорода. Это и есть длина волны спектральной линии в 1420 Мгц между сверхтонкими состояниями. Излучение с такой длиной волны испускается или поглощается атомарным водородным газом в галактиках. Значит, с помощью радиотелескопов, настроенных на волны 21 см (или примерно на 1420 Мгц), можно наблюдать скорости и расположение сгущений атомарного водорода. Измеряя интенсивность, можно оценить его количество. Измеряя сдвиг в частоте, вызываемый эффектом Допплера, можно выяснить движение газа в галактике. Это одна из великих программ радиоастрономии. Так что мы с вами сейчас ведем речь о чем-то очень реальном, это вовсе не какая-то искусственная задача.