§ 1. Уравнение Шредингера для атома водорода

Самым замечательным успехом в истории квантовой механики было объяснение всех деталей спектров простейших атомов, а также периодичностей, обнаруженных в таблице химических элементов. В этой главе в нашем курсе квантовой механики мы наконец-то подойдем к этому важнейшему достижению и расскажем об объяснении спектра атомов водорода. Кроме того, здесь мы расскажем и о качественном объяснении таинственных свойств химических элементов. Для этого мы подробно изучим поведение электрона в атоме водорода: в первую очередь мы рассчитаем его распределения в пространстве, следуя тем представлениям, которые были развиты в гл. 14.

Для полного описания атома водорода следовало бы учесть движения обеих частиц — как протона, так и электрона. В квантовой механике в этой задаче следуют классической идее об описании движения каждой из частиц по отношению к их центру тяжести. Однако мы не будем этого делать. Мы просто используем приближение, в котором протон считается очень тяжелым, настолько тяжелым, что он как бы закреплен в центре атома.

Мы сделаем еще и другое приближение: забудем, что у электрона имеется спин и что его надлежит описывать законами релятивистской механики. Это потребует внесения небольших поправок в наши выкладки, поскольку мы будем пользоваться нерелятивистским уравнением Шредингера и пренебрежем магнитными эффектами. Небольшие магнитные эффекты появляются из-за того, что протон с точки зрения электрона есть циркулирующий по кругу заряд, который создает магнитное поле. В этом поле энергия электрона будет различна, смотря по тому, направлен ли его спин вверх или вниз по полю. Энергия атома должна немного сдвинуться относительно той величины, которую мы вычислим. Но мы пренебрежем этим слабым сдвигом энергии, т. е. вообразим, что электрон в точности подобен волчку, движущемуся в пространстве по кругу и сохраняющему все время одинаковое направление спина. Поскольку речь будет идти о свободном атоме в пространстве, полный момент количества движения будет сохраняться. В нашем приближении будет считаться, что момент количества движения, вызываемый спином электрона, остается неизменным, так что оставшийся момент количества движения атома (то, что обычно называют «орбитальным» моментом количества движения) тоже не будет меняться. В очень хорошем приближении можно считать, что электрон движется в атоме водорода как частица без спина — его орбитальный момент количества движения постоянен.

В этих приближениях амплитуда того, что электрон будет обнаружен в том или ином месте пространства, может быть представлена как функция положения электрона в пространстве и времени. Обозначим амплитуду того, что электрон будет обнаружен в точке х, у, z в момент t через ?(x, у, z, t). Согласно квантовой механике, скорость изменения этой амплитуды со временем дается гамильтоновым оператором, действующим на ту же функцию. Из гл. 14 мы знаем, что

(17.1)

где

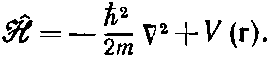(17.2)

Здесь m—масса электрона, а V(r)— потенциальная энергия электрона в электростатическом поле протона. Считая на больших удалениях от протона V=0, можно написать[79]

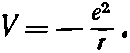
Волновая функция ? должна тогда удовлетворять уравнению

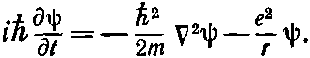(17.3)

Мы хотим найти состояния с определенной энергией, поэтому попробуем поискать решения, которые бы имели вид

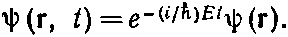(17.4)

Тогда функция ?(r) должна быть решением уравнения

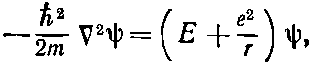(17.5)

где Е — некоторое постоянное число (энергия атома).

Раз потенциальная энергия зависит только от радиуса, то это уравнение лучше решать в полярных координатах.

Лапласиан в прямоугольных координатах определялся так:

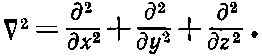
Вместо этого мы хотим воспользоваться координатами r,?, ?, изображенными на фиг. 17.1.

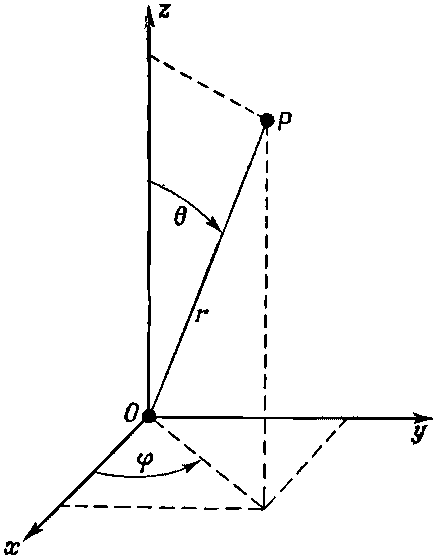
Фиг. 17.1. Сферические координаты r, ?, ? точки Р.

Они связаны с х, у, z формулами

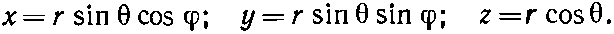
Вас ждут довольно нудные алгебраические выкладки, но в конце концов вы должны будете прийти к тому, что для произвольной функции f(r)=f(r, ?, ?):

(17.6)

Итак, в полярных координатах уравнение, которому должна удовлетворять функция ?(r, ?, ?), принимает вид

(17.7)