Сила – вектор

Сила – вектор

Сила, так же как и скорость, есть векторная величина. Ведь она всегда действует в определенном направлении. Значит, и силы должны складываться по тем правилам, которые мы только что обсуждали.

Мы часто наблюдаем в жизни примеры, иллюстрирующие векторное сложение сил. На рис. 8 показан канат, на котором висит тюк. Веревкой человек оттягивает тюк в сторону. Канат натянут действием двух сил: силы тяжести тюка и силы человека.

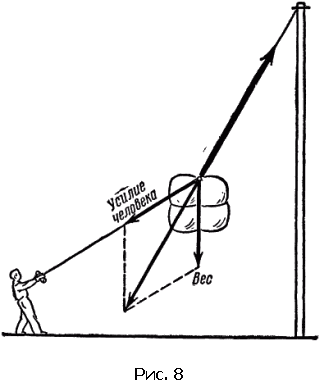
Правило векторного сложения сил позволяет определить направление каната и вычислить силу его натяжения. Тюк находится в покое; значит, сумма действующих на него сил должна равняться нулю. А можно сказать и так – натяжение каната должно равняться сумме силы тяжести тюка и силы тяги в сторону, осуществляемой при помощи веревки. Сумма этих сил даст диагональ параллелограмма, которая будет направлена вдоль каната (ведь иначе она не сможет «уничтожиться» силой натяжения каната). Длина этой стрелки должна будет изображать силу натяжения каната. Такой силой можно было бы заменить две силы, действующие на тюк. Векторную сумму сил поэтому иногда называют равнодействующей.

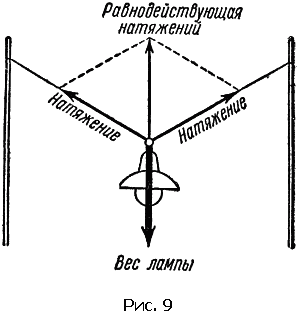
Очень часто возникает задача, обратная сложению сил. Лампа висит на двух тросах. Для того чтобы определить силы натяжения тросов, вес лампы надо разложить по этим двум направлениям.

Из конца равнодействующего вектора (рис. 9) проведем линии, параллельные тросам, до пересечения с ними. Параллелограмм сил построен. Измеряя длины сторон параллелограмма, находим (в том же масштабе, в котором изображен вес) величины натяжений канатов.

Такое построение называется разложением силы. Всякое число можно представить бесконечным множеством способов в виде суммы двух или нескольких чисел; то же можно сделать и с вектором силы: любую силу можно разложить на две силы – стороны параллелограмма, – из которых одну всегда можно выбрать какой угодно. Ясно также, что к каждому вектору можно пристроить любой многоугольник.

Часто бывает удобным разложить силу на две взаимно перпендикулярные – одну вдоль интересующего нас направления и другую перпендикулярно к этому направлению. Их называют продольной и нормальной (перпендикулярной) составляющей силы.

Составляющую силы по какому-то направлению, построенную разложением по сторонам прямоугольника, называют еще проекцией силы на это направление.

Ясно, что на рис. 10

F² = F_прод² + F_норм²,

где F_прод и F_норм – проекция силы на выбранное направление и нормаль к нему.

Знающие тригонометрию без труда установят, что

F_прод = F·cos ?,

где ? – угол между вектором силы и направлением, на которое она проецируется.

Очень любопытным примером разложения сил является движение корабля под парусами. Каким образом удается идти под парусами против ветра? Если вам приходилось наблюдать за парусной яхтой в этом случае, то вы могли заметить, что она движется зигзагами. Моряки называют такое движение лавированием.

Прямо против ветра идти на парусах, конечно, невозможно, но почему удается идти против ветра хотя бы под углом?

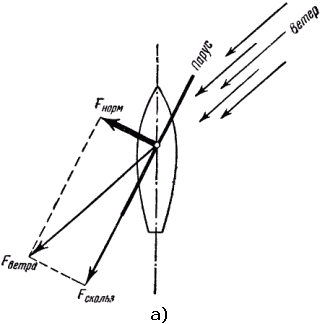
Возможность лавировать против ветра основывается на двух обстоятельствах. Во-первых, ветер толкает парус всегда под прямым углом к его плоскости. Посмотрите на рис. 11,а: сила ветра разложена на две составляющие – одна из них заставит воздух скользить вдоль паруса, другая – нормальная составляющая – оказывает давление на парус. Во-вторых, лодка движется не туда, куда ее толкает сила ветра, а туда, куда смотрит нос лодки.

Это объясняется тем, что движение лодки поперек килевой линии встречает очень сильное сопротивление воды. Значит, чтобы лодка двигалась носом вперед, надо, чтобы сила давления на парус имела бы составляющую вдоль килевой линии, смотрящую вперед.

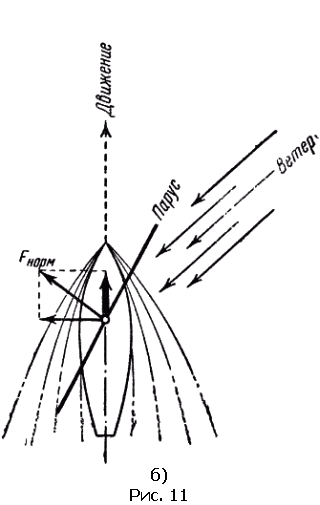
Теперь рис. 11,б, на котором изображена идущая против ветра лодка, должен стать понятным вам. Парус устанавливают так, чтобы его плоскость делила пополам угол между направлением хода лодки и направлением ветра.

Для того чтобы найти силу, которая гонит лодку вперед, силу ветра придется разложить дважды. Сначала вдоль и перпендикулярно к парусу – имеет значение лишь нормальная составляющая, затем эту нормальную составляющую надо разложить вдоль и поперек килевой линии. Продольная составляющая и гонит лодку под углом к ветру.