Изменение давления с высотой
Изменение давления с высотой
С изменением высоты давление падает. Впервые это было выяснено французом Перье по поручению Паскаля в 1648 г. Гора Пью де Дом, около которой жил Перье, была высотой 975 м. Измерения показали, что ртуть в торричеллиевой трубке падает при подъеме на гору на 8 мм. Вполне естественно падение давления воздуха с увеличением высоты. Ведь наверху на прибор уже давит меньший столб воздуха.
Если вы летали в самолете, то знаете, что на передней стенке кабины помещен прибор, показывающий с точностью до десятков метров высоту, на которую поднялся самолет. Прибор называется альтиметром. Это обычный барометр, но проградуированный на значения высот над уровнем моря.
Давление падает с возрастанием высоты; найдем формулу этой зависимости. Выделим небольшой слой воздуха площадью в 1 см2, расположенный между высотами h1 и h2. В не очень большом слое изменение плотности с высотой мало заметно. Поэтому вес выделенного объема (это цилиндрик высотой h2 ? h1 и площадью 1 см2) воздуха будет mg = ?(h2 ? h1)g. Этот вес и дает падение давления при подъеме с высоты h1 на высоту h2. То есть
Но по закону Бойля – Мариотта плотность газа пропорциональна давлению. Поэтому
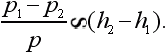
Слева стоит доля, на которую возросло давление при снижении с h2 до h1. Значит, одинаковым снижениям h2 ? h1 будет соответствовать прирост давления на один и тот же процент.
Измерения и расчет показывают в полном согласии, что при подъеме над уровнем моря на каждый километр давление будет падать на 0,1 долю. То же самое относится и к спуску в глубокие шахты под уровень моря – при опускании на один километр давление будет возрастать на 0,1 долю своего значения.
Речь идет об изменении на 0,1 долю от значения на предыдущей высоте. Это значит, что при подъеме на один километр давление уменьшается до 0,9 от давления на уровне моря, при подъеме на следующий километр оно становится равным 0,9 от 0,9 давления на уровне моря; на высоте в 3 километра давление будет равно 0,9 от 0,9 от 0,9, т.е. (0,9)3 давления на уровне моря. Нетрудно продлить это рассуждение и далее.
Обозначая давление на уровне моря через p0, можем записать давление на высоте h (выраженной в километрах):
p = p0(0,87)h = p0·10?0,06h.
В скобках записано более точное число: 0,9 – это округленное значение. Формула предполагает температуру одинаковой на всех высотах. На самом же деле температура атмосферы меняется с высотой и притом по довольно сложному закону. Тем не менее формула дает неплохие результаты, и на высотах до сотни километров ею можно пользоваться.
Нетрудно определить при помощи этой формулы, что на высоте Эльбруса – около 5,6 км – давление упадет примерно вдвое, а на высоте 22 км (рекордная высота подъема стратостата с людьми) давление упадет до 50 мм Hg.
Когда мы говорим про давление 760 мм Hg – нормальное, не нужно забывать добавить: «на уровне моря». На высоте 5,6 км нормальным давлением будет не 760, а 380 мм Hg.
Вместе с давлением по тому же закону падает с возрастанием высоты и плотность воздуха. На высоте 160 км воздуха останется маловато.
Действительно,
(0,87)160 = 10?10.
У земной поверхности плотность воздуха равна примерно 1000 г/м3, значит, на высоте 160 км на один, кубический метр должно приходиться по нашей формуле 10?7 г воздуха. На самом же деле, как показывают измерения, произведенные при помощи ракет, плотность воздуха на этой высоте раз в десять больше.
Еще большее занижение против истины дает наша формула для высот в несколько сот километров. В том, что формула становится непригодной на больших высотах, виновато изменение температуры с высотой, а также особое явление – распад молекул воздуха под действием солнечного излучения. Здесь мы не станем на этом останавливаться.