VI. Движение твердых тел

VI. Движение твердых тел

Момент силы

Попробуйте рукой привести во вращение тяжелое маховое колесо. Тяните за спицу. Вам будет тяжело, если вы ухватитесь рукой слишком близко к оси. Переместите руку к ободу, и дело пойдет легче.

Что же изменилось? Ведь сила в обоих случаях одна и та же. Изменилась точка приложения силы.

Во всем предыдущем изложении вопрос о месте приложения силы не возникал, так как в рассмотренных задачах форма и размер тела роли не играли. По сути дела мы мысленно заменяли тело точкой.

Пример с вращением колеса показывает, что вопрос о точке приложения силы далеко не праздный, когда речь идет о вращении или повороте тела.

Для того чтобы понять роль точки приложения силы, вычислим работу, которую надо проделать, чтобы повернуть тело на некоторый угол. При этом расчете, конечно, предполагается, что все частички твердого тела жестко сцеплены между собой (мы оставляем пока без внимания способность тела гнуться, сжиматься – вообще менять свою форму). Поэтому сила, приложенная к одной точке тела, сообщает кинетическую энергию всем его частям.

При вычислении этой работы роль точки приложения сил отчетливо видна.

На рис. 49 показано закрепленное на оси тело. При повороте тела на маленький угол ? точка приложения силы переместилась по дуге – прошла путь s.

Проектируя силу на направление движения, т.е. на касательную к окружности, по которой движется точка приложения, напишем знакомое выражение работы A:

A = F_прод·s

Но дуга s может быть представлена как

s = r?,

где r – расстояние от оси вращения до точки приложения силы. Итак,

A = F_прод·r?.

Поворачивая тело на один и тот же угол разными способами, мы можем затратить различную работу в зависимости от того, где приложена сила.

Если угол задан, то работа определяется произведением F_прод·r. Такое произведение называют моментом силы:

M = F_прод·r

Формуле момента силы можно придать другой вид. Пусть O – ось вращения и B – точка приложения силы (рис. 50). Буквой d обозначена длина перпендикуляра, опущенного из O на направление силы. Два треугольника, построенные на рисунке, подобны. Поэтому

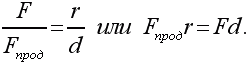
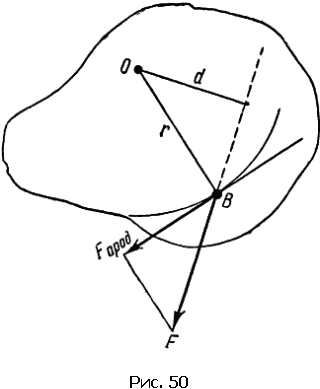
Величина d называется плечом силы. Новая формула M = Fd читается так: момент силы равен произведению силы на ее плечо.

Если точку приложения силы перемещать вдоль направления силы, то плечо d, а вместе с ним и момент силы не будут меняться. Значит, безразлично, где именно на линии силы лежит точка приложения.

При помощи нового понятия формула для работы запишется короче:

A = M?,

т.е. работа равняется произведению момента силы на угол поворота.

Пусть на тело действуют две силы с моментами M₁ и M₂. При повороте тела на угол ? будет совершена работа M₁? + M₂? = (M₁ + M₂)?. Эта краткая запись показывает, что две силы с моментами M₁ и M₂ вращают тело так, как это делала бы одна сила с моментом M, равным сумме M₁ + M₂. Моменты сил могут как помогать, так и мешать друг другу. Если моменты M₁ и M₂ стремятся повернуть тело в одну и ту же сторону, то мы должны считать их величинами, имеющими одинаковый алгебраический знак. Напротив, моменты сил, поворачивающие тело в разные стороны, имеют разные знаки.

Как мы знаем, работа всех сил, действующих на тело, идет на изменение кинетической энергии.

Вращение тела замедлилось или ускорилось – значит, изменилась его кинетическая энергия. Это может произойти лишь в том случае, если суммарный момент сил не равен нулю.

А если суммарный момент равен нулю? Ответ ясен – кинетическая энергия не изменяется, следовательно, тело или вращается равномерно по инерции, или покоится.

Итак, равновесие способного вращаться тела требует уравновешивания действующих на него моментов сил. Если действуют две силы, равновесие требует равенства

M₁ + M₂ = 0.

Пока нас интересовали такие задачи, в которых тело можно было рассматривать как точку, условия равновесия были проще: чтобы тело покоилось или двигалось равномерно, говорил закон Ньютона для таких задач, надо, чтобы результирующая сила равнялась нулю; силы, действующие вверх, должны уравновеситься силами, направленными вниз; сила вправо должна компенсироваться силой влево.

Этот закон действителен и для нашего случая. Если маховое колесо находится в покое, то действующие на него силы уравновешиваются реакцией оси, на которую насажено колесо.

Но этих необходимых условий становится недостаточно. Кроме уравновешивания сил требуется еще уравновешивание моментов сил. Уравновешивание моментов является вторым необходимым условием покоя или равномерного вращения твердого тела.

Моменты сил, если их много, без труда разбиваются на две группы: одни стремятся вращать тело вправо, другие – влево. Эти-то моменты и должны компенсироваться.