Энергия тяготения

Энергия тяготения

На простом примере мы уже познакомились с энергией тяготения. Тело, поднятое на высоту h над землей, обладает потенциальной энергией mgh.

Однако этой формулой можно пользоваться лишь тогда, когда высота h много меньше радиуса Земли.

Энергия тяготения – важная величина, и интересно получить формулу ее, которая годилась бы для тела, поднятого на любую высоту над землей, а также вообще для двух масс, притягивающихся по универсальному закону:

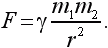
Положим, что под действием взаимного притяжения тела немного сблизились. Между ними было расстояние r₁, а стало r₂. При этом совершается работа A = F(r₁ – r₂). Значение силы надо взять в какой-то средней точке. Итак,

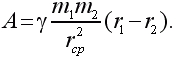
Если r₁ и r₂ мало отличаются друг от друга, то можно заменить r_ср² произведением r₁r₂. Получаем:

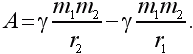
Эта работа произведена за счет энергии тяготения:

A = U₁ ? U₂,

где U₁ – начальное, а U₂ – конечное значение потенциальной энергии тяготения.

Сопоставляя эти две формулы, находим для потенциальной энергии выражение

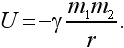
Оно похоже на формулу силы тяготения, но в знаменателе стоит r в первой степени.

По этой формуле при очень больших r потенциальная энергия U = 0. Это разумно, так как на таких расстояниях притяжение уже не будет чувствоваться. Но при сближении тел потенциальная энергия должна уменьшаться. Ведь за ее счет происходит работа.

А куда же уменьшаться от нуля? В отрицательную сторону. Поэтому в формуле и стоит минус. Ведь ?5 меньше нуля, а ?10 меньше ?5.

Если речь идет о движении около земной поверхности, то общее выражение силы тяготения можно заменить произведением mg. Тогда с большой точностью U₁ ? U₂ = mgh.

Но на поверхности Земли тело имеет потенциальную энергию ??(Mm/R), где R – радиус Земли. Значит, на высоте h над земной поверхностью

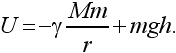
Когда мы впервые ввели формулу потенциальной энергии U = mgh, было условлено высоту и энергию отсчитывать от земной поверхности. Пользуясь формулой U = mgh, мы отбрасываем постоянный член ??(Mm/R), условно считаем его равным нулю. Так как нас интересуют лишь разности энергий – ведь обычно измеряется работа, которая есть разность энергий, – то присутствие постоянного члена ??(Mm/R) в формуле потенциальной энергии роли не играет.

Энергия тяготения определяет прочность цепей, «привязывающих» тело к Земле. Как порвать эти цепи, как добиться того, чтобы брошенное с Земли тело не вернулось на Землю? Ясно, что для этого нужно придать телу большую начальную скорость. Но каково же минимальное требование?

По мере отдаления от Земли потенциальная энергия выброшенного с Земли тела (снаряда, ракеты) будет расти (абсолютное значение U падает); кинетическая энергия будет падать. Если кинетическая энергия тела станет равной нулю преждевременно, до того как мы оборвем цепи тяготения земного шара, выброшенный снаряд упадет обратно на Землю.

Необходимо, чтобы тело сохраняло кинетическую энергию до тех пор, пока его потенциальная энергия практически не упадет до нуля. Перед отправлением снаряд обладал потенциальной энергией ??(Mm/R) (M и R – масса и радиус Земли). Поэтому снаряду нужно дать такую скорость, которая сделала бы полную энергию оторвавшегося снаряда положительной. Тело с отрицательной полной энергией (абсолютное значение потенциальной энергии больше значения кинетической) не выберется за пределы сферы тяготения.

Таким образом, мы приходим к простому условию. Для того чтобы тело массы m оторвать от Земли, надо, как уже сказано, преодолеть потенциальную энергию тяготения

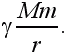
Скорость снаряда должна быть при этом доведена до значения так называемой второй космической скорости v₂, которую легко вычислить из равенства кинетической и потенциальной энергий:

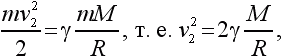
или, так как g = ?(M/R²),

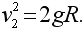
Значение v₂, вычисляемое по этой формуле, составляет 11 км/с, – конечно, без учета сопротивления атмосферы. Эта скорость в sqrt(2) = 1,41 раза больше первой космической скорости v₁ = sqrt(gR) искусственного спутника, вращающегося около земной поверхности, т.е. v₂ = sqrt(2)·v₁.

Масса Луны в 81 раз меньше массы Земли; радиус ее меньше земного в четыре раза. Поэтому энергия тяготения на Луне в двадцать раз меньше, чем на Земле, и для отрыва от Луны достаточно скорости 2,5 км/с.

Кинетическая энергия mv₂²/2 тратится на то, чтобы порвать цепи тяготения к планете – отправной станции. Если же мы хотим, чтобы, преодолев тяготение, ракета двигалась со скоростью v, то на это нужна дополнительная энергия mv²/2. В этом случае, посылая ракету в путешествие, необходимо сообщить ей энергию mv₀²/2 = mv₂²/2 + mv²/2.

Таким образом, три скорости, о которых идет речь, связаны простым соотношением:

v₀² = v₂² + v².

Чему же должна равняться скорость v₃, нужная для преодоления тяготения Земли и Солнца, – минимальная скорость снаряда, посылаемого к далеким звездам? Эту скорость мы обозначили v₃, потому что ее называют третьей космической скоростью.

Определим прежде всего значение скорости, необходимой для преодоления одного лишь притяжения Солнца.

Как мы только что показали, скорость, нужная для выхода из сферы земного притяжения снаряда, отправляемого в путешествие, в sqrt(2) раз больше, чем скорость вывода на орбиту земного спутника. Эти рассуждения в равной степени относятся и к Солнцу, т.е. скорость, нужная для ухода от Солнца, в sqrt(2) раз больше, чем скорость спутника Солнца (т.е. Земли). Поскольку скорость движения Земли вокруг Солнца составляет примерно 30 км/с, то скорость, необходимая для ухода из сферы притяжения Солнца, равна 42 км/с. Это очень много, однако для отправления снаряда к далеким звездам надо, разумеется, использовать движение земного шара и запускать тело в ту сторону, куда движется Земля. Тогда нам нужно добавить всего 42 ? 30 = 12 км/с.

Теперь мы можем окончательно вычислить третью космическую скорость. Это скорость, с которой надо вывести ракету, чтобы, выйдя из сферы земного притяжения, она имела скорость 12 км/с. Воспользовавшись формулой, приведенной только что, получим:

v₃² = (11)² + (12)²,

откуда v₃ = 16 км/с.

Итак, имея скорость около 11 км/с, тело покинет Землю, но «далеко» такой снаряд не уйдет; Земля его отпустила, но Солнце не даст ему свободы. Он превратится в спутника Солнца.

Оказывается, что скорость, необходимая для межзвездного путешествия, всего лишь в полтора раза больше скорости, нужной для путешествия по солнечной системе внутри земной орбиты. Правда, как уже говорилось, всякое заметное увеличение начальной скорости снаряда сопряжено с немалыми техническими трудностями (см. стр. 82).