Центр тяжести

Центр тяжести

Все частички тела обладают весом. Поэтому твердое тело находится под действием бесчисленного количества сил тяжести. При этом все эти силы параллельны. Если так, то их можно сложить по правилам, которые мы только что рассматривали, и заменить одной силой. Точка приложения суммарной силы называется центром тяжести. В этой точке как бы сосредоточен вес тела.

Подвесим тело за одну из его точек. Как оно при этом расположится? Поскольку мы можем мысленно заменить тело одним сосредоточенным в центре тяжести грузом, ясно, что в равновесии этот груз будет лежать на вертикали, проходящей через точку опоры. Другими словами, в равновесии центр тяжести лежит на вертикали, проходящей через точку опоры, и находится в самом низком положении.

Можно расположить центр тяжести на вертикали, проходящей через ось, и над точкой опоры. Это удастся сделать с большим трудом и только благодаря наличию трения. Такое равновесие неустойчиво.

Мы уже говорили об условии устойчивого равновесия – потенциальная энергия должна быть минимальна. Так оно и есть в том случае, когда центр тяжести лежит ниже точки опоры. Любое отклонение повышает центр тяжести и, значит, увеличивает потенциальную энергию. Напротив, когда центр тяжести лежит над точкой опоры, то любое дуновение, выводящее тело из этого положения, ведет к уменьшению потенциальной энергии. Такое положение неустойчиво.

Вырежем из картона фигуру. Для того чтобы найти центр ее тяжести, подвесим ее два раза, приклеивая нитку-подвес сначала в одной, а потом в другой точке тела. Закрепим фигуру на оси, проходящей через центр тяжести. Повернем фигуру в одно положение, второе, третье… Мы обнаружим полное безразличие тела к нашим операциям. В любом положении осуществляется специальный случай равновесия. Его так и называют – безразличным.

Причина этого ясна – при любом положении фигуры заменяющая ее материальная точка находится в одном и том же месте.

В ряде случаев центр тяжести можно найти и без опыта и вычислений. Ясно, например, что центры тяжести шара, круга, квадрата, прямоугольника находятся в центрах этих фигур, так как они симметричны. Если мысленно разбить симметричное тело на частички, то каждой из них будет соответствовать другая, расположенная симметрично по другую сторону от центра. А для каждой пары таких частиц центр фигуры явится центром тяжести.

У треугольника центр тяжести лежит на пересечении медиан. Действительно, разобьем треугольник на узенькие полоски, параллельные одной из сторон. Медиана делит пополам каждую из полосок. Но центр тяжести полоски лежит, конечно, посередине полоски, т.е. на медиане. Центры тяжести всех полосок попадают на медиану, и когда мы будем складывать их силы веса, мы придем к выводу, что центр тяжести треугольника лежит где-то на медиане. Но это рассуждение верно в отношении любой из медиан. Поэтому центр тяжести должен лежать на их пересечении.

Но, может быть, вы не уверены, что три медианы пересекаются в одной точке. Это доказывается в геометрии; но наше рассуждение тоже доказывает эту интересную теорему. Ведь у тела не может быть несколько центров тяжести; а раз он один и лежит он на медиане, из какого бы угла мы ее ни провели, то значит, все три медианы пересекаются в одной точке. Постановка физического вопроса помогла нам доказать геометрическую теорему. Труднее найти центр тяжести однородного конуса. Из соображений симметрии ясно только, что центр тяжести лежит на осевой линии. Расчет показывает, что он находится на расстоянии 1/4 высоты от основания. Центр тяжести не обязательно находится внутри тела. Например, центр тяжести кольца находится в его центре, т.е. вне кольца.

Можно ли устойчиво поставить на стеклянной подставке булавку в вертикальном положении?

На рис. 57 показано, как это сделать. Небольшое сооружение из проволоки в виде двойного коромысла с четырьмя маленькими грузиками надо жестко прикрепить к булавке. Так как грузики подвешены ниже опоры, а вес булавки мал, то центр тяжести лежит ниже точки опоры. Положение устойчиво.

До сих пор речь шла о телах, имевших точку опоры. А что будет, если тело опирается на целую площадку?

Ясно, что в этом случае расположение центра тяжести над опорой вовсе не говорит о неустойчивости равновесия. Как иначе могли бы стоять стаканы на столе? Для устойчивости нужно, чтобы линия действия силы тяжести, проведенная из центра тяжести, проходила через площадь опоры. Наоборот, если линия действия силы проходит вне площади опоры, то тело падает.

Степень устойчивости может быть очень различной в зависимости от того, как высоко расположен центр тяжести над опорой. Стакан с чаем опрокинет только очень неловкий человек, а вот цветочную вазу с маленьким основанием можно опрокинуть неосторожным прикосновением. В чем здесь дело?

Взгляните на рис. 58. Одна и та же опрокидывающая сила, складываясь с силой тяжести, дает суммарную силу, которая прижимает тело к опоре, если центр тяжести расположен низко, а при высоко расположенном центре тяжести суммарная сила не проходит через площадь опоры, а направлена в сторону.

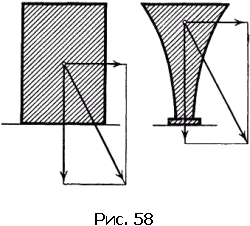
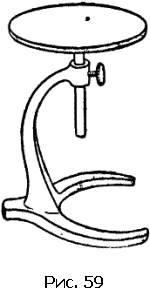
Мы сказали, что для устойчивости тела приложенная к нему сила должна пройти через площадь опоры. Но площадь опоры, нужная для равновесия, не всегда соответствует фактической площади опоры. На рис. 59 изображено тело, площадь опоры которого имеет форму полумесяца. Легко сообразить, что устойчивость тела не изменится, если полумесяц дополнить до сплошного полукруга. Таким образом, площадь опоры, определяющая условие равновесия, может быть больше фактической.

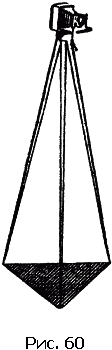
Чтобы найти опорную площадь для изображенного на рис. 60 треножника, надо его концы соединить отрезками прямых.

Почему так трудно ходить по канату? Потому, что площадь опоры резко уменьшается. Ходить по канату нелегко, и не даром награждают аплодисментами искусного канатоходца. Однако иногда зрители впадают в ошибку и признают за вершину искусства хитрые трюки, облегчающие задачу. Артист берет сильно изогнутое коромысло с двумя ведрами воды; ведра оказываются на уровне каната. С серьезным лицом, при замолкшем оркестре, артист совершает переход по канату. Как усложнен трюк, думает неопытный зритель. На самом же деле артист облегчил свою задачу, понизив центр тяжести.