Путь пули

Путь пули

Задача бросить предмет как можно дальше решается человеком с незапамятных времен. Камень, брошенный рукой или выпущенный из рогатки, стрела, вылетевшая из лука, ружейная пуля, артиллерийский снаряд, баллистическая ракета – вот краткий перечень успехов в этой области.

Брошенный предмет движется по кривой линии, называемой параболой. Ее можно построить без труда, если движение брошенного тела рассматривать как сумму двух движений – по горизонтали и по вертикали, происходящих одновременно и независимо. Ускорение силы тяжести вертикально, поэтому летящая пуля движется по горизонтали по инерции с постоянной скоростью и одновременно по вертикали с постоянным ускорением падает на Землю. Как же сложить эти два движения?

Начнем с простого случая – начальная скорость горизонтальна (скажем, речь идет о выстреле из ружья, ствол которого горизонтален).

Возьмем лист миллиметровой бумаги и проведем вертикальную и горизонтальную линии (рис. 15). Так как оба движения происходят независимо, то через t секунд тело переместится на отрезок v₀t вправо и на отрезок gt²/2 вниз. Отложим по горизонтали отрезок v₀t и из конца его – вертикальный отрезок gt²/2. Конец вертикального отрезка укажет точку, в которой окажется тело через t секунд.

Это построение надо сделать для нескольких точек, т.е. для нескольких моментов времени. Через эти точки пройдет плавная кривая – парабола, изображающая траекторию тела. Чем чаще будут отложены точки, тем точнее будет построена траектория полета пули.

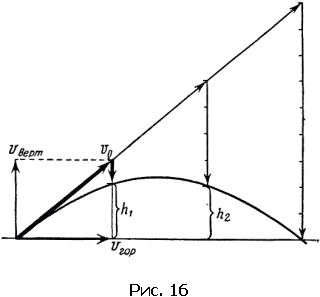
На рис. 16 построена траектория для случая, когда начальная скорость v₀ направлена под углом.

Вектор v₀ следует прежде всего разложить на вертикальную и горизонтальную составляющие. На горизонтальной линии будем откладывать v_горt – путь, на который сдвинется пуля вдоль горизонтали через t секунд.

Но пуля совершает одновременно движение вверх.

Через t секунд тело поднимется на высоту h = v_вертt ? gt²/2.

По этой формуле, подставляя в нее интересующие нас моменты времени, надо рассчитать вертикальные смещения и отложить их на вертикальной оси. Сначала величины h будут возрастать (подъем), а затем убывать.

Теперь остается нанести на график точки траектории так же, как мы это сделали в предыдущем примере, и провести через них плавную кривую.

Если держать ствол ружья горизонтально, то пуля быстро зароется в землю; при вертикальном положении ствола она упадет на то место, откуда был произведен выстрел. Значит, чтобы стрелять как можно дальше, нужно ствол ружья установить под каким-то углом к горизонту. Но под каким?

Используем опять тот же прием – разложим вектор начальной скорости на две составляющие: по вертикали скорость равна v₁, а по горизонтали – v₂. Время от момента выстрела до момента достижения пулей наивысшей точки пути равно v₁/g. Обратим внимание на то, что столько же времени пуля будет падать вниз, т.е. полное время полета до падения пули на землю есть 2v₁/g.

Так как движение по горизонтали равномерное, то дальность полета равна

(при этом мы пренебрегли высотой ружья над уровнем земли).

Мы получили формулу, которая показывает, что дальность полета пропорциональна произведению составляющих скорости. При каком же направлении выстрела это произведение будет наибольшим? Этот вопрос можно выразить на языке геометрии. Скорости v₁ и v₂ образуют прямоугольник скоростей; диагональю в нем служит полная скорость v. Произведение v₁v₂ равно площади этого прямоугольника.

Наш вопрос сводится к следующему: при заданной длине диагонали какие надо взять стороны, чтобы площадь прямоугольника была наибольшей? В геометрии доказывается, что этому условию удовлетворяет квадрат. Значит, дальность полета пули будет наибольшей, когда v₁ = v₂, т.е. тогда, когда прямоугольник скоростей обращается в квадрат. Диагональ квадрата скоростей образует с горизонталью угол в 45° – под таким углом и надо держать ружье, чтобы пуля летела как можно дальше.

Если v – полная скорость пули, то в случае квадрата v₁ = v₂ = v/sqrt(2). Формула дальности полета для этого лучшего случая выглядит так: S = v²/g, т.е. дальность будет вдвое больше, чем высота подъема при выстреле вверх с той же начальной скоростью.

Высота подъема при выстреле под углом в 45° будет h = v₁²/2g = v²/4g, т.е. в четыре раза меньше дальности полета.

Надо признаться, что формулы, которыми мы оперировали, дают точные результаты лишь в случае, довольно далеком от практики, – при отсутствии воздуха. Сопротивление воздуха во многих случаях играет решающую роль и в корне меняет всю картину.