Столкновения
Столкновения
При всяком столкновении двух тел всегда сохраняется импульс. Что же касается энергии, то она, как мы только что выяснили, обязательно уменьшится из-за различного рода трения.
Однако, если сталкивающиеся тела сделаны из упругого материала, например из кости или стали, то потеря энергии будет незначительной.
Такие столкновения, при которых суммы кинетических энергий до и после столкновения одинаковы, называются идеально упругими.
Небольшая потеря кинетической энергии происходит и при столкновении самых упругих материалов – у костяных биллиардных шаров она достигает, например, 3–4 %.
Сохранение кинетической энергии при упругом ударе позволяет решить ряд задач.
Рассмотрим, например, лобовое столкновение шаров разной массы. Уравнение импульса имеет вид (мы считаем, что шар № 2 покоился до удара)
m1v1 = m1u1 + m2u2,
а энергии –
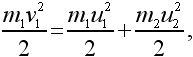
где v1 – скорость первого шара до столкновения, а u1 и u2 – скорости шаров после столкновения.
Так как движение происходит вдоль прямой линии (проходящей через центры шаров – это и означает, что удар лобовой), то применять векторные обозначения здесь не обязательно.
Из первого уравнения имеем:
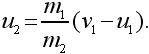
Подставляя это выражение для u2 в уравнение энергии, получим:
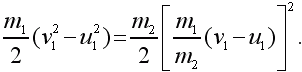
Одним из решений этого уравнения является решение u1 = v1 и u2 = 0. Но этот ответ нас не интересует, так как равенства u1 = v1 и u2 = 0 означают, что шары вовсе не сталкивались. Поэтому ищем другое решение уравнения.
Сократив на m1(v1 ? u1), получим:
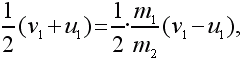
т.е.
m2v1 + m2u1 = m1v1 ? m1u1
или
(m1 ? m2)v1 = (m1 + m2)u1,
что дает следующее значение для величины скорости первого шара после удара:

При лобовом столкновении с неподвижным шаром налетающий шар отскакивает обратно (u1 отрицательно), если его масса меньше. Если m1 больше m2, то оба шара продолжают движение в направлении удара.
При биллиардной игре в случае точного лобового удара часто наблюдается такая картина: шар-снаряд резко останавливается, шар-мишень отправляется в лузу. Это объясняется только что найденным уравнением. Массы шаров равны, и уравнение дает u1 = 0, а значит, u2 = v1. Налетающий шар останавливается, а второй шар начинает движение со скоростью налетевшего. Шары как бы меняются скоростями.
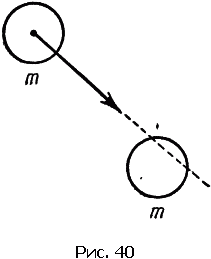
Рассмотрим еще один пример столкновения тел по закону упругого удара, а именно косой удар тел равной массы (рис. 40). Второе тело до удара покоилось, поэтому законы сохранения импульса и энергии имеют вид:
mv1 = mu1 + mu2,
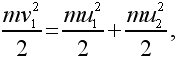
Сократив на массу, получим:
v1 = u1 + u2, v12 = u12 + u22.
Вектор v1 есть векторная сумма u1 и u2. Но ведь это означает, что длины векторов-скоростей образуют треугольник.
Что же это за треугольник? Вспомним теорему Пифагора. Ее выражает наше второе уравнение. Это значит, что треугольник скоростей должен быть прямоугольным с гипотенузой v1 и катетами u1 и u2. Значит, u1 и u2 образуют между собой прямой угол. Этот интересный результат показывает, что при любом косом упругом ударе тела равной массы разлетаются под прямым углом.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
7.5. Эллипс рассеяния в плоскости цели. Оценка вероятности столкновения
7.5. Эллипс рассеяния в плоскости цели. Оценка вероятности столкновения Только один виртуальный астероид пересекает плоскость цели в момент, когда Земля находится у одного конца кратчайшего отрезка между орбитами. Другие виртуальные астероиды, движущиеся вдоль
9.2. Оценки риска погибнуть в результате столкновения небесного тела с Землей
9.2. Оценки риска погибнуть в результате столкновения небесного тела с Землей Зная частоту ударов, мы можем рассчитать и средний промежуток времени между ударами тел данного диаметра. Для определенного тела можно оценить размер зоны разрушений и, используя данные о
9.4. Палермская техническая шкала для оценки угрозы столкновения Земли с астероидами и кометами
9.4. Палермская техническая шкала для оценки угрозы столкновения Земли с астероидами и кометами Туринская шкала, рассмотренная в предыдущем разделе, была разработана прежде всего для описания и распространения сведений об астероиднокометной опасности средствами