Закон всемирного тяготения

Закон всемирного тяготения

Первый вопрос, который задал себе Ньютон, был таков: чем отличается ускорение Луны от ускорения яблока? Иначе говоря, каково различие между ускорением g, которое земной шар создает на своей поверхности, т.е. на расстоянии r от центра, и ускорением, создаваемым Землей на расстоянии R, на котором находится Луна от Земли?

Чтобы подсчитать это ускорение v²/R, надо знать скорость движения Луны и ее расстояние от Земли. Обе эти цифры были Ньютону известны. Ускорение Луны оказалось равным примерно 0,27 см/с². Это приблизительно в 3600 раз меньше значения g = 980 см/с².

Значит, создаваемое Землей ускорение уменьшается с удалением от центра Земли. Но как быстро? Расстояние равно шестидесяти земным радиусам. Но 3600 есть квадрат 60. Увеличив расстояние в 60 раз, мы уменьшили ускорение в (60)² раз.

Ньютон сделал вывод, что ускорение, а значит и сила тяготения, изменяется обратно пропорционально квадрату расстояния. Далее, мы уже знаем, что сила, действующая на тело в поле тяжести, пропорциональна его массе. Поэтому первое тело притягивает второе с силой, пропорциональной массе второго тела; второе тело притягивает первое с силой, пропорциональной массе первого тела.

Речь идет о тождественно равных силах – силах действия и противодействия. Значит, сила взаимного тяготения должна быть пропорциональна массе как первого, так и второго тела, иначе говоря – произведению масс.

Итак,

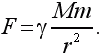
Это и есть закон всемирного тяготения. Ньютон предположил, что такой закон будет верен для любой пары тел.

Теперь эта смелая гипотеза полностью доказана. Таким образом, сила притяжения двух тел прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.

А что это за ?, которая вошла в формулу? Это коэффициент пропорциональности. Нельзя ли считать его равным единице, как мы это уже неоднократно делали? Нет, нельзя: мы условились измерять массу в граммах, расстояние в сантиметрах, а силу в динах. Значение ? равно силе притяжения между двумя массами в 1 г, находящимися на расстоянии 1 см. Мы не можем считать силу равной чему-то, в том числе и одной дине: коэффициент ? должен быть измерен.

Чтобы найти ?, разумеется, не обязательно промерять силы притяжения граммовых гирек. Мы заинтересованы в том, чтобы произвести измерение над массивными телами – тогда сила будет побольше.

Если определить массу двух тел, знать расстояние между ними и измерить силу притяжения, то ? найдется простым расчетом.

Такие опыты ставились много раз. Они показали, что значение ? всегда одно и то же, независимо от материала притягивающихся тел, а также от свойств среды, в которой они находятся. ? называется гравитационной постоянной. Она равна

? = 6,67·10^?8 см³/(г·с²)

Схема одного из опытов по измерению ? показана на рис. 64. К концам коромысла весов подвешены два шарика одинаковой массы. Один из них находится над свинцовой плитой, другой – под ней. Свинец (для опыта взято 100 т свинца) увеличивает своим притяжением вес правого шарика и уменьшает вес левого. Правый шарик перевешивает левый. По величине отклонения коромысла весов вычисляется значение ?.

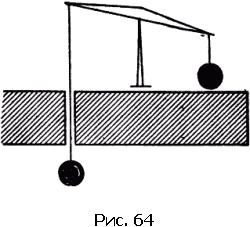
Незначительной величиной ? объясняется трудность обнаружения силы тяготения между двумя предметами.

Два тяжелых 1000-килограммовых груза тянутся друг к другу с ничтожной силой, равной всего лишь 6,7 дин, т.е. 0,007 Г, если эти предметы находятся, скажем, на расстоянии 1 м один от другого.

Но как велики силы притяжения между небесными телами! Между Луной и Землей

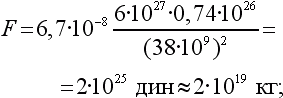
между Землей и Солнцем