Как движутся планеты

Как движутся планеты

На вопрос, как движутся планеты, можно ответить кратко: повинуясь закону тяготения. Ведь силы тяготения – единственные силы, приложенные к планетам.

Так как масса планет много меньше массы Солнца, то силы взаимодействия между планетами не играют большой роли. Каждая из планет движется почти так, как это диктует ей сила притяжения одного лишь Солнца, словно других планет и не существует.

Законы движения планеты вокруг Солнца следуют из закона всемирного тяготения.

Впрочем, исторически дело было не так. Законы движения планет были найдены замечательным немецким астрономом Иоганном Кеплером до Ньютона без помощи закона тяготения на основании почти двадцатилетней обработки астрономических наблюдений.

Пути, или, как говорят астрономы, орбиты, которые описывают планеты около Солнца, очень близки к окружностям.

Как связан период обращения планеты с радиусом ее орбиты?

Сила тяготения, действующая на планету со стороны Солнца, равна

где М – масса Солнца, m – масса планеты, r – расстояние между ними.

Но F/m есть, согласно основному закону механики, не что иное, как ускорение, и притом центростремительное:

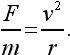
Скорость планеты можно представить как длину окружности 2?r, поделенную на период обращения T. Подставив v = 2?R/T и значение силы F в формулу ускорения, получим:

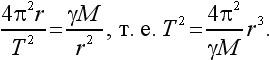
Коэффициент пропорциональности перед r³ есть величина, зависящая только от массы Солнца, – одинаковая для любой планеты. Следовательно, для двух планет справедливо соотношение

Отношение квадратов времен обращения планет оказывается равным отношению кубов радиусов их орбит. Этот интересный закон был выведен Кеплером из опыта. Закон всемирного тяготения объяснил наблюдения Кеплера.

Круговое движение одного небесного тела около другого – это лишь одна из возможностей.

Траектории одного тела, вращающегося около другого благодаря силам тяготения, могут быть самыми различными. Однако, как показывает расчет и как еще до всякого расчета было обнаружено Кеплером, все они принадлежат к одному классу кривых, называемых эллипсами.

Если привязать нитку к двум булавкам, воткнутым в лист чертежной бумаги, натянуть нитку острием карандаша и двигать карандашом так, чтобы нитка оставалась натянутой, то на бумаге в конце концов прочертится замкнутая кривая – это и есть эллипс (рис. 68). Места, где находятся булавки, будут фокусами эллипса.

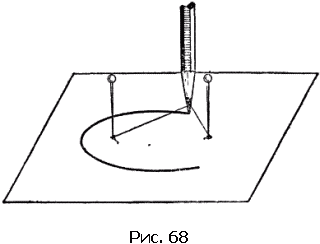
Эллипсы могут иметь различную форму. Если взять нитку много длиннее, чем расстояние между булавками, то эллипс будет очень похож на круг. Напротив, если длина нитки чуть-чуть больше расстояния между булавками, то получится удлиненный эллипс – почти палочка.

Планеты описывают эллипсы, в одном из фокусов которых находится Солнце.

Какие же эллипсы описывают планеты? Оказывается, очень близкие к окружности.

Наиболее отличен от окружности путь ближайшей к Солнцу планеты – Меркурия. Но и в этом случае самый длинный диаметр эллипса всего лишь на 2 % больше самого короткого. Иное дело орбиты искусственных планет. Посмотрите на рис. 69. Орбиту Марса не отличишь от круга.

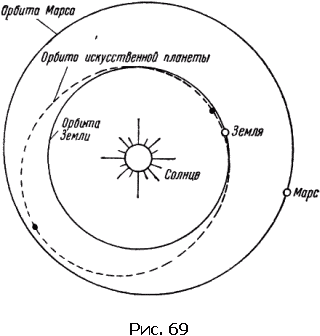
Однако Солнце находится в одном из фокусов эллипса, а не в его центре, и поэтому расстояние планеты от Солнца меняется сильнее. Проведем линию через два фокуса эллипса – она пересечет эллипс в двух местах. Точку, ближайшую к Солнцу, называют перигелием, наиболее далекую от Солнца – афелием. Меркурий, когда находится в перигелии, в 1,5 раза ближе к Солнцу, чем в афелии.

Главные планеты описывают вокруг Солнца эллипсы, близкие к окружности. Однако существуют небесные тела, которые движутся около Солнца по сильно вытянутым эллипсам. К ним принадлежат кометы. Их орбиты не идут ни в какое сравнение по вытянутости с орбитами планет. Про небесные тела, движущиеся по эллипсам, можно сказать, что они принадлежат к семье Солнца. Однако в нашу систему забредают и случайные пришельцы.

Наблюдались кометы, описывающие около Солнца такие кривые, судя по форме которых можно было сделать вывод: комета не вернется, она не принадлежит к семейству солнечной системы. «Открытые» кривые, описываемые кометами, называются гиперболами.

Особенно быстро движутся такие кометы, когда они проходят около Солнца. Это и понятно – полная энергия кометы постоянна, а подходя к Солнцу, комета имеет наименьшую потенциальную энергию. Значит, кинетическая энергия движения будет в этом случае наибольшая. Конечно, такой эффект имеет место для всех планет и для нашей Земли. Однако эффект этот невелик, так как мала разница потенциальных энергий в афелии и перигелии.

Интересный закон движения планеты вытекает из закона сохранения момента импульса.

На рис. 70 изображено два положения планеты. От Солнца, т.е. от фокуса эллипса, проведены два радиуса к положениям планеты, и образовавшийся сектор заштрихован. Надо определить величину площади, описываемой радиусом за единицу времени. При небольшом угле сектор, описанный радиусом за секунду, можно заменить треугольником. Основание треугольника – скорость v (путь, проходимый за секунду), а высота треугольника равна плечу d скорости. Поэтому площадь треугольника есть vd/2.

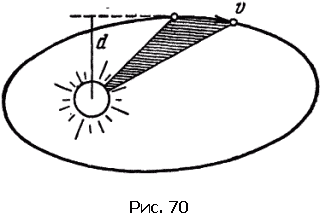
Из закона сохранения момента следует постоянство величины mvd во время движения. Но если mvd неизменно, то не меняется и площадь треугольника vd/2. Мы можем начертить секторы для любых моментов времени – они окажутся одинаковыми по площади. Скорость планеты меняется, но то, что можно назвать секториальной скоростью, остается неизменным.

Не все звезды имеют планетное окружение. Довольно много в небе двойных звезд. Два огромных небесных тела вращаются одно около другого.

Огромная масса Солнца делает его центром семейства. В двойных звездах оба небесных тела имеют близкие по величине массы. В этом случае нельзя считать, что одна из двух звезд покоится. Как же происходит движение в этом случае? Мы знаем, что каждая замкнутая система имеет одну покоящуюся (или равномерно движущуюся) точку – это центр инерции. Вокруг этой точки и вращаются обе звезды. При этом они описывают подобные эллипсы, что следует из написанного на стр. 135 условия m₁/m₂ = r₂/r₁.

Эллипс одной звезды больше эллипса другой во столько раз, во сколько масса одной звезды больше массы другой (рис. 71). При равных массах обе звезды будут описывать около центра инерции одинаковые траектории.

Планеты солнечной системы находятся в идеальных условиях: они не подвержены трению.

Создаваемые людьми маленькие искусственные небесные тела – спутники – не находятся в таком идеальном положении: силы трения, пусть сначала очень незначительные, но все же чувствительные, решительно вмешиваются в их движение.

Полная энергия планеты остается неизменной. Полная энергия спутника с каждым оборотом слегка падает. На первый взгляд кажется, что трение будет замедлять движение спутника. В действительности происходит обратное.

Вспомним прежде всего, что скорость спутника равна

sqrt(gR) или sqrt(?(M/R)), где R – расстояние от центра Земли, а М – ее масса.

Полная энергия спутника равна:

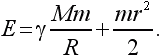
Подставив значение скорости спутника, найдем для кинетической энергии выражение ?(mM/2R). Мы видим, что по абсолютной величине кинетическая энергия в два раза меньше потенциальной, а полная энергия равна

При наличии трения полная энергия будет падать, т.е. (поскольку она отрицательна) расти по абсолютной величине; расстояние R начнет уменьшаться: спутник снижается. Что при этом произойдет со слагаемыми энергии? Потенциальная энергия убывает (растет по абсолютной величине), кинетическая энергия растет.

Общий баланс все же отрицателен, так как потенциальная энергия убывает вдвое быстрее, чем возрастает кинетическая.

Трение приводит к возрастанию скорости движения спутника, а не к замедлению.

Теперь понятно, почему большая ракета-носитель обгоняет маленький спутник. У большой ракеты трение больше.