§ 3. Синусоидальные волны.

Зафиксируем вначале r и рассмотрим поле как функцию времени. Получается функция, которая осциллирует с угловой частотой ?. Угловую частоту со можно определить как скорость изменения фазы со временем (радианы в секунду). Эта величина нам уже знакома. Период есть время одного колебания, одного полного цикла; он равен 2?/?, так как произведение ? и периода есть полный период косинуса.

Введем новую величину, которая очень часто используется в физике. Она возникает в другой ситуации, когда t фиксировано и волна рассматривается как функция расстояния r. Легко увидеть, что как функция r волна (29.3) тоже осциллирует. Если отвлечься от множителя 1/r, то мы видим, что Е тоже осциллирует, когда мы меняем положение. Тогда по аналогии с ? введем так называемое волновое число и обозначим его через k. Оно определяется как скорость изменения фазы с расстоянием (радианы на метр). Время при таком изменении остается фиксированным.

Роль периода здесь играет другая величина, ее можно было бы назвать периодом в пространстве, однако ее обычное название — длина волны, а обозначается она буквой ?. Длина волны есть расстояние, на котором колебание поля совершает один полный цикл. Легко видеть, что длина волны равна 2?/k, потому что k, умноженное на длину волны, равно полному периоду косинуса. Итак, соотношение k?=2? полностью аналогично ?t₀=2?.

В нашем конкретном случае между частотой и длиной волны имеется определенная связь, однако приведенные выше определения k и ? носят совершенно общий характер и применимы также в тех физических условиях, когда никакого соотношения между этими величинами нет. Для рассматриваемой нами волны скорость изменения фазы с расстоянием найти легко. В самом деле, запишем выражение для фазы ?=?(t-r/с) и возьмем частную производную по r

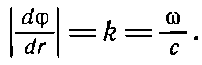(29.4)

Это соотношение можно записать разными способами:

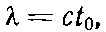(29.5)

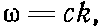(29.6)

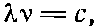(29.7)

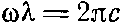(29.8)

Почему длина волны оказывается равной периоду, умноженному на c? Очень просто. Дело в том, что за время, равное одному периоду, волны, двигаясь со скоростью с, пройдут расстояние ct₀, а, с другой стороны, это расстояние должно быть равно длине волны.

В других физических явлениях, когда приходится иметь дело не со светом, такого простого соотношения между k и ? может и не быть. Пусть волна движется вдоль оси x, тогда распространение синусоидальной волны с частотой ? и волновым числом k описывается общей формулой вида sin(?t-kx).

Введенное понятие длины волны позволяет уточнить пределы применимости формулы (29.1). Напомним, что поле складывается из нескольких частей: одна из них спадает как 1/r, другая — как 1/r², а остальные падают с расстоянием еще быстрее. Имеет смысл выяснить: когда часть, спадающая по закону 1/r, наиболее существенна, а остальными можно пренебречь? Естественно ответить: «Когда мы отойдем достаточно далеко от источника, потому что член 1/r² будет мал по сравнению с членом 1/r». Но что значит «достаточно далеко»? В общих чертах ответ таков: все остальные члены имеют порядок величины ?/r по сравнению с первым членом 1/r. Так что когда мы находимся на расстоянии нескольких длин волн от источника, формула (29.1) описывает поле в хорошем приближении. Область, удаленную от источника на расстояние, превышающее несколько длин волн, иногда называют «волновой зоной».