§ 5. Теорема об энергии

Энергия волны пропорциональна квадрату ее амплитуды. Для сложной волны энергия за один период пропорциональна ₀?^Tf²(t)dt. Эту энергию можно связать с коэффициентами Фурье. Напишем

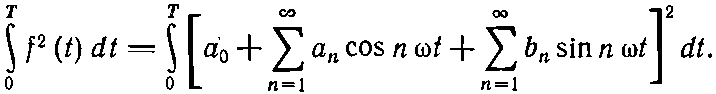(50.22)

После раскрытия квадрата в правой части мы получим сумму всевозможных перекрестных членов типа a₅cos5?tb₇cos7?t. Однако выше мы уже показали [уравнения (50.11) и (50.12)], что интегралы от всех таких членов по одному периоду равны нулю, так что останутся только квадратные члены, подобные a²₅cos²5?t. Интеграл от любого квадрата косинуса или синуса по одному периоду равен Т/2, так что получаем

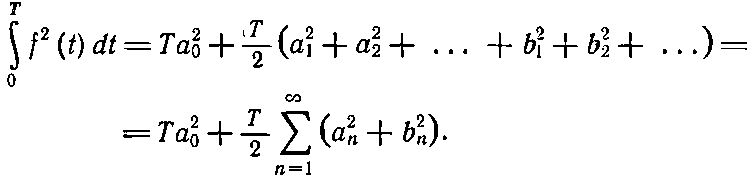(50.23)

Это уравнение называют «теоремой об энергии», которая говорит, что полная энергия волны равна просто сумме энергий всех ее фурье-компонент. Применяя, например, эту теорему к ряду (50.19), мы получаем

поскольку [f(t)]²=1. Таким образом мы узнали, что сумма квадратов обратных нечетных чисел равна ?²/8. Точно так же, выписав сначала ряд Фурье для функции и используя затем теорему об энергии, можно доказать результат, понадобившийся нам в гл. 45, т. е. что 1+¹/2⁴+¹/3⁴+... равно ?⁴/90.