§ 7. Четырехвектор (ω, k)

Соотношения (34.17) и (34.18) обладают весьма интересным свойством: новая частота ?' линейно связана со старой частотой ? и старым волновым числом k, а новое волновое число представляется в виде комбинации старого волнового числа и частоты. Далее, волновое число есть скорость изменения фазы с расстоянием, а частота — скорость изменения фазы со временем, и сами соотношения обнаруживают глубокую аналогию с преобразованиями Лоренца для координаты и времени: если ? сопоставить с t, а k с х/с², то новое ?' сопоставляется с t', a k' — с координатой х'/с². Иначе говоря, при преобразовании Лоренца ? и k изменяются так же, как t и х. Эти величины ? и k составляют так называемый четырехвектор. Четырехкомпонентная величина, преобразующаяся как время и координаты, и есть четырехвектор. Здесь все правильно, за исключением одного — четырехвектор имеет четыре компоненты, а у нас фигурируют только две! Как уже говорилось, ? и k подобны времени и одной координате пространства; для введения двух остальных координат надо изучить распространение света в трехмерном пространстве.

Пусть задана система координат x, y, z и волна движется в пространстве с волновым фронтом (фиг. 34.11). Длина волны есть ?, а направление распространения волны не совпадает ни с одной осью координат.

Фиг. 34.11. Плоская волна, движущаяся под углом.

Какой вид имеет формула движения для такой волны? Ответ очевиден: это cos(?t-ks), где k=2?/ ? a s (расстояние вдоль направления движения волны) — проекция вектора положения на направление движения. Запишем это следующим образом: пусть r есть вектор точки в пространстве, тогда s есть r·е_k, где e_k — единичный вектор в направлении движения волны. Иначе говоря, s равно rcos(r·e_k), проекции расстояния на направление движения. Следовательно, наша волна описывается формулой cos(?t-ke_k·r).

Оказывается очень удобным ввести вектор k, называемый волновым вектором; величина его равна волновому числу 2?/?, а направление совпадает с направлением распространения волны

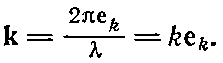(34.19)

Благодаря введению этого вектора волна приобретает вид cos(?t-k·r), или cos(?t-k_xx-k_yy-k_zz). Выясним смысл проекций k, например k_x. Очевидно, k_x есть скорость изменения фазы в зависимости от координаты х. Фиг 34.11 подсказывает нам, что фаза меняется с ростом х так, как если бы вдоль х бежала волна, но соответствующая ей длина волны оказывается больше по величине. «Длина волны в направлении х» больше истинной на множитель, равный секансу угла ? между осью х и направлением движения истинной волны:

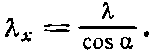(34.20)

Следовательно, скорость изменения фазы, обратно пропорциональная ?_x, в направлении х оказывается меньше на множитель cos?; но этот же множитель содержит и k_x, равный модулю k, умноженному на косинус угла между k и осью х!

Итак, мы выяснили смысл волнового вектора, описывающего распространение волны в трехмерном пространстве. Четыре величины ?, k_x, k_y, k_z преобразуются в теории относительности как четырехвектор, причем ? соответствует времени, а k_x, ky, k_z соответствуют x, y и z и компонентам четырехвектора.

Еще раньше, когда мы занимались теорией относительности (гл. 17), мы выяснили, что из четырехвекторов можно составить релятивистское штрихованное произведение. Взяв вектор положения x_? (где ? нумерует четыре компоненты — время и три пространственные) и волновой вектор k_? (где ? снова пробегает четыре значения), образуем штрихованное произведение х_? и k_?, записываемое в виде ?'k_? х_?. Это произведение есть инвариант, не зависящий от выбора системы координат. Согласно определению штрихованного произведения, можно записать ?'k_?х_?. следующем виде:

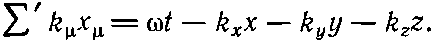(34.21)

Поскольку k_? есть четырехвектор, то, как мы уже знаем, ?'k_?x_? есть инвариант по отношению к преобразованиям Лоренца. Под знак косинуса в нашей формуле для плоской волны входит именно это произведение, и оно обязано быть инвариантом относительно преобразований Лоренца. У нас не может появиться формула, у которой под знаком косинуса стоит неинвариантная величина, потому что мы знаем, что значение фазы не зависит от выбора системы координат.