1.68. Эффект домино

Как только первая костяшка домино из длинного ряда стоящих вертикально на одинаковом расстоянии друг от друга костяшек упадет на соседнюю, падения распространятся, как волна, по всему ряду. Сколько костяшек будет находиться в движении в каждый произвольный момент времени уже после того, как волна пошла, и чем определится скорость распространения этой волны? Расстояние между костяшками, естественно, не должно превышать длину каждой из них. А есть ли еще какой-то параметр, определяющий минимальное расстояние? Почему детские кубики не падают так же, как костяшки? Возникнет ли цепная реакция в ряду костяшек, если первая костяшка маленькая, а каждая следующая больше предыдущей в некоторое количество раз?

ОТВЕТ • Стоящая вертикально костяшка имеет два положения равновесия. Одно из них — когда костяшка стоит на меньшей грани вертикально (рис. 1.23а), а другое — когда она повернулась на небольшой угол относительно этого положения и ее центр масс находится как раз над ребром, на котором костяшка стоит (рис. 1.23б). В обоих положениях сила тяжести, которая, как мы предполагаем, приложена в центре масс костяшки, проецируется на основание костяшки. Однако про второе положение говорят, что в нем костяшка находится в положении неустойчивого равновесия. Действительно, любое малейшее воздействие выводит костяшку из этого положения, поскольку проекция силы тяжести сдвигается влево или вправо от ребра костяшки. Если она сдвигается вправо, как на рис. 1.23в, костяшка опрокинется.

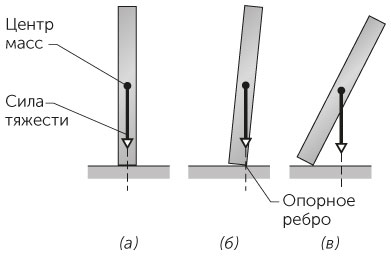
Рис. 1.23 / Задача 1.68. Костяшки домино проходят через положение неустойчивого равновесия.

Когда вы ударяете по первой костяшке в ряду, она пролетает через положение неустойчивого равновесия и падает плашмя на следующую. Если вы просто слегка подтолкнете первую костяшку, энергия от ее падения пойдет на выведение второй костяшки из равновесия. Если расстояние между костяшками мало, время падения на вторую костяшку и переданная ей энергия слишком малы, чтобы уронить и ее. Падение более вероятно при большем расстоянии — конечно, если оно не превышает длины костяшки. То же касается и остальных костяшек в ряду. (Конечно, вы могли бы как следует врезать по первой костяшке и не заботиться о соблюдении нужного расстояния между костяшками, но это будет неспортивно.)

В каждый произвольный момент времени в движении может участвовать пять или шесть костяшек. Волна набирает скорость по мере ее движения вдоль ряда костяшек, и эта скорость приближается к определенному значению, зависящему от расстояния между костяшками, трения между ними и того, как одна из них отскакивает от другой. Когда расстояние меньше, волна движется быстрее, и высота звука, издаваемого костяшками при падении, выше.

Профессор Лорн Вайтхед из Университета Британской Колумбии однажды описал, как цепная реакция распространяется по ряду костяшек домино, если все ребра каждой следующей костяшки в 1,5 раза больше, чем у предыдущей. Он опрокинул первую костяшку, «толкнув ее длинным тонким ватным жгутиком», а к моменту, когда опрокинулась тринадцатая костяшка, энергия в этой цепной реакции возросла в 2 миллиарда раз. Он посчитал, что в более длинном ряду таких же костяшек понадобилось бы только 32 штуки, чтобы снести «костяшку» размером с Эмпайр-стейт-билдинг. (Такого не сделал бы и Кинг-Конг.)