Спектральный ряд

Однако как ни хороша теория Льюиса — Ленгмюра, она объясняет структуру лишь простейших химических соединений. С ее помощью невозможно объяснить, например, структуру гидрида бора (соединения бора и водорода) или свойства бензола (С₆Н₆). Также невозможно объяснить и поведение элементов с атомными числами меньше, чем у кальция, или почему так схожи свойства лантаноидов, хотя их атомные числа разнятся от 57 до 71.

Слабым местом во взглядах Льюиса и Ленгмюра является то, что ученые рассматривали электроны как неподвижные частицы, занимающие внутри атома строго определенные места. Действительно, на рисунках того времени электроны оболочек L и М располагались по восьми углам куба, а молекулы простейших соединений состояли из нескольких таких кубов, соединенных вместе.

Конечно же такое представление удобно с химической точки зрения, но абсолютно неприемлемо с физической. Ведь если отрицательно заряженный электрон висит над положительно заряженным ядром неподвижно, то он должен просто-напросто упасть на ядро. (Точно так же Земля упала бы на Солнце, если бы не вращалась вокруг него.)

Постепенно физики пришли к выводу, что электрон, чтобы не упасть на ядро, вращается вокруг него с огромной скоростью. В 1904 году японский физик Хантаро Нагаока предположил, в частности, что электроны движутся вокруг ядра так же, как планеты движутся по своим орбитам вокруг Солнца[123].

Впрочем, все модели атомов, где электроны вращались вокруг ядра, сталкивались с одной и той же проблемой. Вращающийся вокруг ядра электрон постоянно испытывает центростремительное ускорение, а согласно теории Максвелла постоянно ускоряющийся заряд должен постоянно испускать электромагнитное излучение.

Именно такую модель и создал Нагаока. Электрон, двигающийся вокруг ядра, и является этим зарядом и должен испускать излучение определенной частоты (как и в случае с искрами у Герца, см. гл. 2). Если электрон в минуту совершает 500 триллионов оборотов вокруг ядра (а это всего лишь 150 километров в секунду), то частота его излучения будет 500 триллионов Гц, а это в пределах видимой части спектра, ведь свет — это тоже электромагнитное излучение.

Предположение, конечно, красивое, но разрушить его все-таки придется. Если вращающийся электрон будет испускать излучение постоянно, то он будет терять энергию, а единственной энергией, которой обладает электрон, является кинетическая (т. е. энергия движения). Соответственно движение электрона вокруг ядра должно постепенно замедляться, а сам электрон будет по спирали приближаться к ядру, пока не остановится окончательно и не притянется ядром[124].

Но раз электроны на ядро не падают, нужно создавать какую-то другую модель. Новая модель должна отражать тот факт, что атомы не только излучают (и поглощают) свет, но излучают и поглощают свет лишь определенной частоты. Для создания модели атома следует изучить взаимосвязи между этими уникальными световыми волнами, а отталкиваться нужно от водорода, поскольку водород излучает волны самого простого и упорядоченного спектра.

Длина волн, образующих самые четкие линии спектра водорода, составляет 656,21 миллимикрона, 486,08 миллимикрона, 434,01 миллимикрона, 396,81 миллимикрона и так далее. Расстояние между линиями уменьшается пошагово, значит, здесь определенно должна быть какая-то закономерность.

В 1885 году немецкий математик Иоганн Якоб Бальмер (1825–1898) вывел простую формулу, по которой можно рассчитать длину этих волн:

? = 364,56m²/(m² – 4), (Уравнение 5.1)

где m может быть любым целым числом начиная с 3. Если m = 3, то ? будет равна 656,21 миллимикрона, т. е. длине первой волны водородного спектра. Если подставлять вместо m числа 4, 5, 6, то ? будет равна длине второй, третьей и четвертой линии водородного спектра. Эти линии получили название серия Бальмера.

С возрастанием значения m значение m² ? 4 знаменателя будет практически равно значению m² числителя, и дробь сократится. В этом случае ? будет равно 364,56 миллимикрона (постоянная Бальмера). Именно к этому значению длины волны стремятся все линии серии Бальмера.

Через несколько лет шведский физик Юханнес Роберт Ридберг (1854–1919), преобразовав формулу Бальмера, сделал ее более удобной. Сначала он написал возвратное уравнение:

1/? = (m² – 4)/(364,56m²). (Уравнение 5.2)

Затем, умножив знаменатель и числитель дроби в правой части формулы 5.2 на 4, получил:

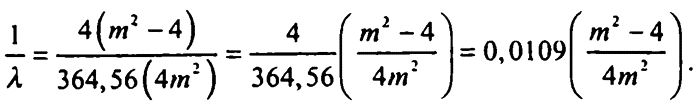
Давайте рассмотрим каждый член правой части формулы 5.3 по отдельности. Число 0,0109 получается делением 4 на бальмерову константу. Это значение в миллимикронах. Ридберг предпочел использовать сантиметры, а раз в одном сантиметре 10 000 000 миллимикрон, то значение в сантиметрах будет 0,0109?10 000 000 = 109 (современные измерения дают значение 109 737 31). Это число получило название постоянная Ридберга и обозначается как R. Таким образом, в пересчете на сантиметры формула 5.3 будет выглядеть так:

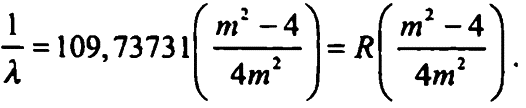
Получаем значение ? в сантиметрах, т. е. длина основной волны равна 0,000065621 см.

Теперь разложим (m² – 4)/4m² на m²/4m² – 4/4m² и сократим до 1/4 — 1/m². Для симметрии представим 4 как 1/2² – 1/m², тогда формула 5.4 приобретает вид:

1/? = R?(1/2² - 1/m²), (Уравнение 5.5)

где m — любое целое число, равное и большее 3.

Формулы оставшихся линий будут выглядеть аналогично:

1/? = R?(1/1² - 1/m²), (Уравнение 5.6)

1/? = R?(1/3² - 1/m²), (Уравнение 5.7)

1/? = R?(1/4² - 1/m²) (Уравнение 5.8)

и так далее. Значением m для формулы 5.6 должно быть любое целое число больше 1, для формулы 5.7 — больше 3, для формулы 5.8 — больше 4.

Формула 5.6 описывает волны ультрафиолетового спектра. Эти волны короче волн серии Бальмера. Они были открыты в 1906 году американским физиком Теодором Лайманом и получили название волны серии Лаймана.

Формула 5.7 описывает волны инфракрасного спектра. Они длиннее волн серии Бальмера. Они были открыты в 1908 году немецким физиком Фридрихом Пашеном и получили название серия Пашена. Формула 5.8 описывает еще более длинные волны, открытые американским физиком Фредериком Брэкеттом и получившие названия серия Брэкетта. Существуют также и другие серии волн.