Увеличение

Любой, кто имел дело с собирающими линзами, прекрасно знает, что предмет, на который глядишь сквозь них, кажется больше. Похоже, что это знали уже в древности, потому что такой же эффект достигается и просто с помощью стеклянного сосуда округлой формы, в который налили воду.

Чтобы понять это, нужно сначала уяснить, что мы не воспринимаем истинные размеры предмета напрямую, а лишь судим о них по набору косвенных признаков, среди которых — угол, под которым падает свет от краев предмета.

Например, допустим, что в 25 см от глаз горизонтально держат палочку длиной 4 см. Угол между лучами света, попадающими в глаз с одного и с другого концов палочки, составляет 9,14°. Другими словами, если мы посмотрим прямо на один конец палочки, а затем повернем голову, чтобы посмотреть прямо на другой, нам придется повернуть ее на 9,14°. Это угол зрения, или угловой диаметр предмета.

Если бы палочка была только два сантиметра длиной, то угол зрения составил бы 4,58°, а для восьмисантиметровой палочки — 18,8°. Угол зрения не совсем пропорционален размеру, но при небольших значениях — почти. На собственном опыте мы познаем эти пропорции и автоматически оцениваем относительный размер предметов по углу зрения.

Однако угловой размер предмета также зависит и от расстояния. Допустим, что восьмисантиметровая палочка, находясь на расстоянии 25 см, занимает угол зрения в 18,18°. На расстоянии 50 см угол зрения будет уже 9,14°, а на расстоянии 100 см — 4,58°. Другими словами, мы также хорошо знаем по собственному опыту, что чем дальше предмет отстоит от глаза, тем меньше он кажется. Большой предмет, отстоящий далеко от глаза, будет выглядеть меньше, чем маленький, находящийся близко к глазу. Так, восьмисантиметровая палочка, отстоящая от глаза на 100 см, будет занимать угол зрения меньше, чем четырехсантиметровая, находящаяся на расстоянии 25 см, и соответственно будет выглядеть меньше.

Не похоже, чтобы это могло ввести нас в заблуждение. С малых лет мы приучаемся принимать в расчет при оценке истинных размеров предмета не только угол зрения, но и расстояние. Для того чтобы, взглянув сперва на отдаленную восьмисантиметровую палочку, посмотреть потом на приближенную четырехсантиметровую, наш глаз должен изменить хрусталик, а также оба наших глаза должны изменить направление взгляда, чтобы оба они сфокусировались на одном и том же предмете (чем ближе предмет, тем сильнее глазам надо скоситься к переносице). Нам не обязательно надо осознавать, что наши хрусталики изменяются или что взгляд сходится к переносице; мы просто правильно оцениваем эти ощущения и можем сделать из них вывод, что четырехсантиметровая палочка находится ближе. Приняв это во внимание наряду с углом зрения, мы обычно без проблем можем сделать вывод, что палочка, кажущаяся меньше, на самом деле больше. Мы даже можем убедить себя, что она и выглядит больше.

Изменения в приспособлении хрусталика и сведение глаз используются, когда речь идет о сравнительно близких предметах. Глядя же на удаленные предметы, мы оцениваем расстояние в сравнении с соседними предметами, размер которых мы знаем. Так, далекая секвойя может не показаться нам особенно большой, пока мы не увидим у ее подножия крохотного человека. Тогда мы понимаем, насколько далеко она находится, и ее подлинный размер становится очевидным. Она начинает казаться большой.

Если рядом с далеким предметом пет предметов известного размера, с которыми его можно было бы сравнить, нам остается только угол зрения, который сам по себе мало что дает. К примеру, Луна в небе занимает, грубо округляя, 0,5°. Если мы попытаемся исходя из этого высчитать подлинный диаметр Луны, мы окажемся в замешательстве. Можно сделать вывод, что Луна «где-то шириной в фут». Однако предмет шириной в фут занимает угол в 0,5°, только если он находится не далее чем в шестидесяти футах. А это уж слишком не соответствует реальному расстоянию до Луны, хотя бессознательно многие считают его именно таковым.

Когда луна висит над горизонтом, то видно, что она находится за домами и деревьями, и мы понимаем, что она явно дальше чем в шестидесяти футах от нас. До нее, должно быть, целая миля. Чтобы занимать угол в 0,5°, находясь на расстоянии в милю, Луна должна быть 88 футов в диаметре. Это (неосознаваемое) изменение нашей оценки удаленности Луны меняет и наше (неосознаваемое же) представление о ее размерах. Как мы все замечали, Луна над горизонтом кажется больше, чем когда она высоко в небе[85]. Эта оптическая иллюзия ставила людей в тупик еще со времен древних греков, но в настоящее время принято считать, что причиной ее является ошибка в бессознательной оценке размера Луны.

Собирательная линза — это возможность изменить угол зрения, не изменяя расстояния до предмета. Представьте себе, что лучи света идут от предмета к глазу и создают определенный угол зрения. Глаз не может почувствовать, что по пути лучи были преломлены; он воспринимает их как прямые линии, идущие от объекта большего, чем тот есть на самом деле. Только воспринимая объект как увеличенный, глаз может обработать больший угол зрения. Или, иначе, глаз видит не предмет, а увеличенное мнимое изображение (сохранившее правильную ориентацию) предмета, создаваемое собирающей линзой. Коэффициент, с которым увеличивается размер предмета, и есть увеличение линзы.

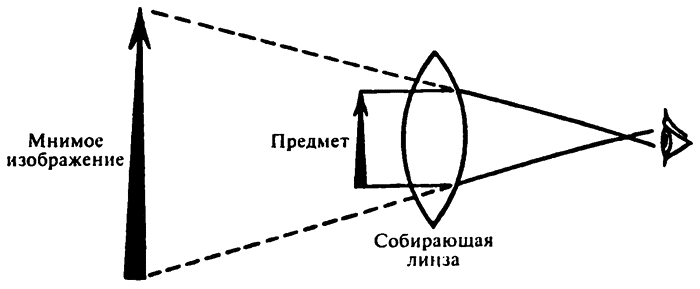
^{Увеличение} 

Если вернуться к формуле линзы (уравнение 2.2 или 3.1), то увеличение может быть выражено через фокусное расстояние линзы (f). Поскольку изображение мнимое, то расстояние до него (D₁) имеет отрицательное значение, в то время как расстояние до самого объекта (D₀) остается, как всегда, положительным. Тогда уравнение может быть приведено к виду:

1/D₀ – 1/D₁ = 1/f. (Уравнение 3.2)

Как я уже сказал, увеличение можно описать как отношение размера изображения к размеру предмета, но об этом отношении можно судить двояко. Можно определить его как отношение углов зрения, занимаемых предметом и изображением на одинаковом расстоянии, а можно — как отношение расстояний, на которых объект и изображение занимают один и тот же угол. Давайте примем последнее определение и решим уравнение 3.2 для отношения расстояний до изображения и до предмета (D₁/D₀). Окажется, что:

D₁/D₀ = f/(f – D₀) = m,

где m и есть увеличение.

Если линзу держат вплотную к предмету, например к странице книги, то D₀ равняется практически нулю и f – D =f. Тогда увеличение m равняется f/f, то есть единице, и буквы не увеличиваются. Когда линзу поднимают, D₀ увеличивается, что приводит к тому, что D₀ должно уменьшаться, и, как мы видим из уравнения 3.3, m, следовательно, должно возрастать. Буквы кажутся все крупнее и крупнее по мере того, как поднимается линза. Когда расстояние от линзы до страницы становится равным фокусному, f – D₀становится равным f – f, или 0. Тогда увеличение по формуле будет f/0, а на практике — бесконечным. Однако идеальных линз не существует, все они несовершенны. В результате изображение будет полностью размыто. Максимум практического увеличения достигается, когда расстояние до предмета становится приближенным к фокусному.

Если предмет находится на расстоянии больше фокусного, f – D₀ становится отрицательным, и соответственно m становится тоже отрицательным. По мере того как D₀ продолжает возрастать, m, оставаясь отрицательным, уменьшается в абсолютном значении (в значении, не зависящем от знака). Это значит, что изображение становится маленьким и перевернутым.

Из уравнения 3.3 следует также, что при фиксированном расстоянии до предмета (D₀) увеличение возрастает с уменьшением фокусного расстояния линзы (при условии, что фокусное расстояние остается большим, чем расстояние до предмета). Чтобы понять это, давайте представим, что D₀ — 1 и что/ последовательно принимает следующие значения: 5, 4, 3 и 2. Поскольку увеличение (т) равняется f/(f – D₀), то оно будет последовательно равным ⁵/₄, ⁴/₃, ³/₂ и ²/₁, или 1,2, 1,33, 1,5 и 2,0. Это еще одна причина, по которой собирающая линза становится более сильной с уменьшением своего фокусного расстояния. В итоге сила ее увеличения возрастает по мере того, как ее фокусное расстояние уменьшается.

С рассеивающими линзами все обстоит так же с точностью до наоборот. Здесь лучи света, сходящиеся на своем пути к глазу, рассеиваются линзой и попадают в глаз под меньшим углом зрения. По этой причине сквозь рассеивающую линзу предметы выглядят маленькими.

Таким образом, можно легко отличить близорукого человека от дальнозоркого по его очкам. Близорукий человек носит рассеивающие линзы, и если эти линзы находятся в нескольких дюймах над книгой, то буквы кажутся меньше. Дальнозоркий же человек носит собирающие линзы, которые делают буквы крупнее.