Вращательное движение

До сих пор я рассматривал движение, как если бы оно вовлекало перемещение объекта через пространство в едином целом с различными частями объекта, поддерживающими их взаимную неизменяемую ориентацию. Такое движение называется «поступательным» (translationat) — от латинских слов, означающих «переносить».

Однако возможно и перемещение тела, при котором оно не будет двигаться через пространство как единое целое, но при этом — все же будет перемещаться. Например, центр колеса может быть закреплен на одном месте, чтобы колесо в целом не изменяло своего положения; однако само колесо может вращаться относительно этого центра. Подобным же образом сфера, установленная в пределах некоторого объема пространства, может вращаться вокруг некоторой установленной линии, оси. Этот вид движения называется «вращательным» (rotational) — от латинского слова, означающего «колесо». (Конечно, тело может двигаться и в комбинации из этих двух типов движения, как это делает бейсбольный мяч, который крутится, одновременно перемещаясь вперед, или как Земля, которая вращается вокруг своей оси, одновременно перемещаясь вперед по своей орбите вокруг Солнца.)

Вращательное движение весьма аналогично поступательному, но рассмотрение его требует изменения точки зрения. Например, мы привыкли думать о скорости поступательного движения в терминах «миля в час» или «сантиметры в секунду», во вращательном движении единицы измерения другие. Кроме того, мы принимаем как очевидное, что если одна часть тела имеет некоторую скорость поступательного движения, то и все остальные части тела имеют такую же скорость. Другими словами — весь самолет перемещается вперед со скоростью своего носа.

В случае вращательного движения эти вопросы различны. Точка на ободе вращающегося колеса перемещается уже с некоторой скоростью, точка, находящаяся ближе к центру колеса, перемещается с меньшей скоростью, а точка, находящаяся еще ближе к центру, перемещается с еще меньшей скоростью. Точка, находящаяся в центре вращающегося колеса, неподвижна. Поэтому сказать, что колесо вращается со скоростью столько-то сантиметров в секунду, является бессмысленным, если мы не указываем точную часть колеса, к которой относится данное высказывание, а это может быть достаточно неудобно.

Было бы более удобно, если бы мы могли найти некоторый метод измерения скорости вращения, который был бы применим сразу ко всему телу вращения. Одним из таких методов может быть рассмотрение числа оборотов тела за единицу времени. Хотя различные точки на колесе могут двигаться с различной скоростью, каждая точка на колесе заканчивает вращение в один и тот же момент времени, так как колесо вращается «как единое целое». Поэтому мы можем говорить о колесе (или любом другом объекте вращения), что оно «имеет скорость в столько-то вращений в минуту» (обычно это выражение сокращают как «об/мин», или «rpm» — от английского «revolutions per minute».

Или мы могли бы разделить одно обращение колеса на 360 равных частей, называемых «градусами» (сокращенно градус обозначается значком °. В этом случае 1 оборот в минуту был бы равен 360 град./мин, или 6 град./с (градусов в секунду). В то время как колесо поворачивается на какой-то градус линия, соединяющая центр колеса с точкой на его ободе, образует угол. Поэтому о скорости, данной в оборотах в минуту или в градусах в секунду, обычно говорят как об «угловой скорости».

Вращательное движение способно совершаться любым из двух зеркально отраженных способов. Если смотреть из некоторого фиксированного положения, то колесо может выглядеть вращающимся «по часовой стрелке», то есть в том же направлении, в котором двигаются стрелки часов. Но с другой стороны, оно может двигаться «против часовой стрелки», то есть в сторону, противоположную движению стрелок часов[25]. Поэтому об угловой скорости можно говорить, учитывая не только величину, но также и направление. (Что касается скоростей, включаемых в поступательное движение, то о них можно говорить как о «линейных скоростях», так как движение тут происходит скорее по линии, чем по углу.)

Физики используют другую единицу измерения вращательной скорости — радиан. Это угол, который отображает на окружности дугу, равную по длине радиусу круга. Длина окружности равна ?, умноженному на диаметр окружности[26], то есть 2? умножить на радиус круга. Поэтому длина окружности равна 2?r, умноженным на длину дуги, обозначенной одним радианом. Один полный оборот заключает в себя прохождение одной полной длины окружности, то есть один оборот равняется 2? радианам, или 360°. Из этого следует, что один радиан равняется 360°/2?, или, так как к равняется 3,14159, один радиан примерно равен 57,3° (1 рад = 57,3°).

Угловая скорость часто обозначается греческой буквой ? («омега»), так как это — греческий эквивалент латинской буквы v, обычно используемой для обозначения линейной скорости.

Для любой данной точки на вращающемся теле угловая скорость может быть приведена к линейной скорости. Линейная скорость зависит не только от угловой скорости, но также и от расстояния, на котором находится рассматриваемая точка от центра вращения (r). Если для той же самой угловой скорости удвоить расстояние от точки до центра вращения, то линейная скорость точки также удвоится. В таком случае можно сказать, что:

v = r?. (Уравнение 6.4)

Это уравнение абсолютно корректно, когда ? измеряется в радианах в единицу времени. Например, если угловая скорость — один радиан в секунду, то за одну секунду данная точка, расположенная на окружности колеса, проходит дугу, равную ее расстоянию от центра, и v = r. ?сли ? равняется 2 радианам в секунду, то v = 2r и так далее.

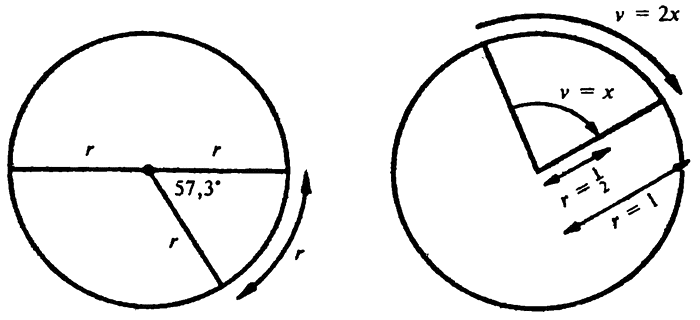
^{а) Величина радиана; б) Угловая скорость}

Если бы мы измеряли ? в оборотах в единицу времени, то уравнение 6.4 можно было бы прочитать как (v = 2?r?), а если бы мы измеряли ее в градусах в единицу времени, то это же уравнение можно было бы прочитать как v = r?/57,3. Это — пример того, как единица измерения, которая на первый взгляд может показаться имеющей странную и неудобную размерность, оказывается весьма полезной, потому что она позволяет выразить отношения между величинами с максимальной простотой.