Умножение силы
Механизм не только передает силу, часто он может использоваться, чтобы умножить эту силу, как мы видим на примере описанного выше рычага. И все же к этому умножению силы нужно относиться с подозрением. Как один ньютон силы может делать работу десяти ньютонов только посредством передачи ее через твердый брусок? Как я указал в начале этой главы, рассчитывать на такое великодушие со стороны Вселенной слишком трудно. Что-то еще должно быть потеряно, чтобы восполнить его.
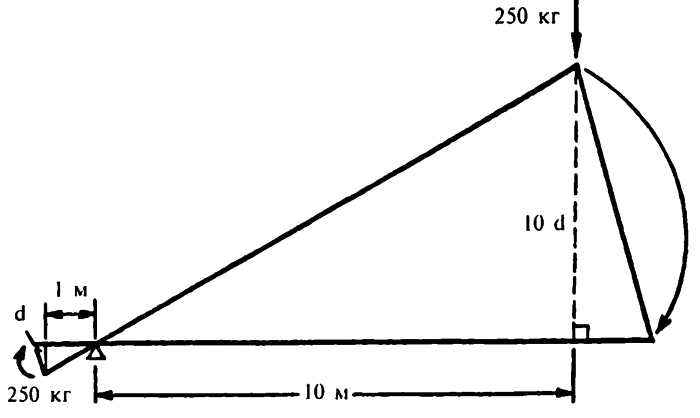
Если мы рассмотрим рычаг, поднимающий вес в 250 килограммов при помощи эквивалента силы, равного только 25 килограммам веса, то, как видно из диаграммы, мы имеем два подобных треугольника. Стороны и высота одного пропорциональны соответствующим сторонам и высоте другого, поскольку расстояние от точки приложения веса до точки опоры пропорционально расстоянию от точки приложения силы до точки опоры.
Другими словами, если мы прикладываем силу в точке, в десять раз так же отдаленной от точки опоры, как вес, а затем поднимаем вес на данное расстояние, мы должны опустить рычаг вниз на расстояние в десять раз большее. Вот он — ответ! При подъеме веса посредством рычага мы можем регулировать расстояния от точки опоры таким образом, чтобы использовать только часть силы, которая потребовалась бы, если бы мы поднимали груз без рычага, но тогда мы должны применить эту часть силы на соответственно большем расстоянии. Произведение силы на расстояние остается тем же самым с обоих концов рычага.
Сила и расстояние
Это оказывается истинным для любого механизма, который, как нам кажется, умножает силу. Меньшая сила исполняет задачу, которая без механизма потребовала бы большей силы, но всегда за счет необходимости приложения этой силы на соответственно большем расстоянии. Произведение силы на перемещение, на котором действует сила, называется «работой» и обычно обозначается w. Таким образом:
w = fd. (Уравнение 7.1)
В некотором смысле работа — достаточно неудачный термин, чтобы использовать его в данной связи. Любой согласится, что подъем веса на какое-то расстояние — работа, но в повседневном использовании смысл данного термина не ограничен одним этим значением. В повседневной речи работа — термин, который применяется к любой форме производства. Если я спокойно сижу в своем кресле и в течение получаса думаю о том, что же дальше написать в этой книге, то такое действие может показаться мне тяжелой работой, но данный процесс не включает в себя какого-либо действия на каком-либо расстоянии, а значит, с точки зрения физика, не является работой. Опять же стоять на одном месте и держать в руке тяжелый чемодан — кажется тяжелой работой, но так как чемодан не двигается, то при этом не совершается никакой работы. Если идете и несете чемодан, то опять же при этом не производится никакой работы, поскольку хотя чемодан и перемещается (горизонтально), но перемещается не в направлении действия силы (вертикально), которая предохраняет его от падения.
Тем не менее термин «работа», означающий силу, умноженную на расстояние, на которое тело перемещается под ее действием, установлен повсеместно и не подлежит переделке.
Единицы измерения работы — это единицы измерения силы, умноженные на единицы измерения расстояния. В системе МКС единицей измерения работы является произведение ньютона на метр; это произведение было названо «джоулем» в честь английского физика, о котором я буду иметь случай упомянуть позже. В системе СГС единица работы получается равной дине, умноженной на сантиметр; эта единица называется «эрг» (от греческого слова, означающего «работа»). Так как ньютон равен 100 000 дин, а метр равен 100 сантиметрам, то ньютон-метр равен 100 000 раз по 100 дин-сантиметров. Другими словами, один джоуль равен 10 000 000 эргов.
Так как сила — векторная величина, может показаться, что работа, которая является произведением силы на расстояние, также должна быть вектором; это означало бы, что можно говорить о данном количестве работы, сделанной при движении направо, и том же количестве работы, сделанной при движении налево, как о равных и противоположных по знаку. Однако это не так. Для того чтобы понять — почему, рассмотрим единицы измерения работы еще раз.
Ньютон определяется как килограммометр в секунду за секунду, или кг-м/с2. Если джоуль равен ньютон-метру, то тогда он равен килограмм-метр-метру в секунду за секунду, или кг-м2/с2. Это последнее выражение может быть записано как кг-(м/с)2. Но м/с (метры в секунду) — единица скорости, а это означает, что единица работы равна единице массы, умноженной на квадрат единицы скорости, или w = mv2.
Истинно, что скорость является векторной величиной, поэтому можно было бы говорить о –v и +v, но единица работы включает в себя квадрат скорости. Как мы знаем из элементарной алгебры, квадрат положительного числа (+v) x (+v) и квадрат отрицательного числа (– v)?(?v) положительны (+v2).
Следовательно, квадрат скорости не показывает никаких различий в знаках, и единица, которая включает в себя квадрат скорости, — не векторная, а скалярная величина (если, конечно, она не содержит других (иных, чем скорость) векторных единиц измерения).
Таким образом, мы пришли к выводу, что работа — скалярная величина.
Возвращаясь к рычагу, мы видим, что работа, потраченная на подъем валуна рычагом, та же самая, что потребовалась бы на подъем валуна без рычага. В данном случае отличается лишь распределение работы между силой и расстоянием. То же самое истинно и в том случае, когда в качестве механизма мы используем наклонную плоскость.
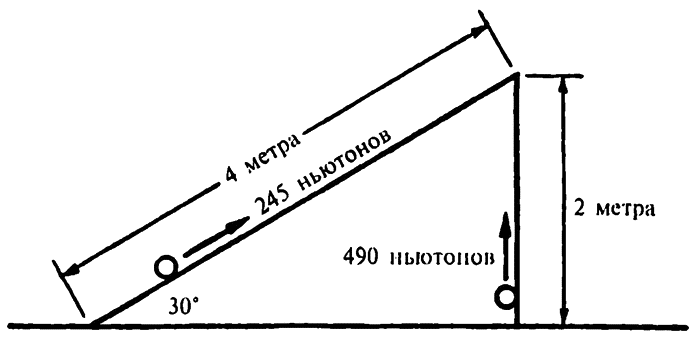
Допустим, что нам необходимо поднять 50-килограммовую бочку на высоту два метра на задний борт грузовика. Так как килограмм веса прикладывает направленную вниз силу, равную 9,8 ньютона, то, чтобы поднять бочку, потребуется сила общей величиной 490 ньютонов. Приложив силу, равную 490 ньютонов, на расстояние в два метра в направлении силы, мы выполним 980 джоулей работы.
Предположим вместо этого, что мы кладем доску от основания (земли) на грузовик таким образом, чтобы доска составляла угол в 30° с землей. При таких условиях длина доски от основания до грузовика только в два раза больше вертикального расстояния от земли до грузовика, или четыре метра. Сила, которая потребуется, чтобы катить бочку по доске, равна 245 ньютонам, то есть только половине силы, требуемой для прямого подъема. Эта половина силы прикладывается на расстоянии в два раза большем, но работа продолжает равняться 980 джоулям.
Наклонная плоскость
Чем меньше угол наклона наклонной плоскости, тем меньше сила, которая потребуется, чтобы переместить бочку, и тем длиннее расстояние, на которое она должна быть перемещена. Наклонная плоскость уменьшает силу так же, как она уменьшала скорость в опыте с силой тяжести, который выполнил Галилео. Ни наклонная плоскость, ни рычаг, ни любой другой механизм не уменьшает работу. Если мы рассматриваем работу, то мы никогда не получаем что-то из ничего.
Но если мы не получаем никаких преимуществ при выполнении работы, то зачем беспокоиться? Ответ состоит в том, что, даже если мы не получаем ничего непосредственно, мы можем извлечь пользу, изменяя распределение между силой и расстоянием. Если рассматриваемый случай — подъем груза, когда мы должны поднять вверх на два метра 250 килограммов, то без дополнительной помощи мы не сможем его поднять и вынуждены будем отказаться. Мы не сможем поднять его на метр, сантиметр или вообще на какую-либо высоту; мы не сможем сдвинуть его. Однако переместить груз, эквивалентный 50 килограммам, на расстояние в десять метров — вполне выполнимая задача, особенно если нам некуда спешить; таким образом, мы можем сделать ту же самую работу (50?10), которая была признана невозможной при предыдущих условиях (250?2). Поднять эквивалент пяти килограммов по наклонной плоскости длиной 100 метров — может быть, утомительно, но вполне возможно.
Опять же если бы нас попросили подтянуться вверх по веревке, спущенной с крыши пятиэтажного здания, то мы могли бы сразу решить, что это — вне пределов наших способностей, разве что мы находимся в превосходной физической форме. Однако совершенно обычный человек может поднять свой вес на крышу пятиэтажного дома, если он идет по скату, который является наклонной плоскостью, позволяющему ему использовать меньшее количество силы, чтобы поднять свое тело за счет перемещения его на более длинное расстояние.
Иногда удобно сделать противоположное: израсходовать дополнительную силу, чтобы получить выигрыш в расстоянии. Именно таким образом мы прикладываем много силы к педали велосипеда. Это усилие передается к точке на заднем колесе, около его центра. Далее спицы колеса действуют как рычаги (с точкой опоры на оси колеса), так что на обод колеса передается небольшая сила, благодаря которой велосипед перемещается на большое расстояние.
Велосипед поэтому — механизм, который позволяет телу преобразовывать силу в расстояние (без изменения полного количества выполненной работы) более эффективно, чем это могло быть сделано без велосипеда. По этой причине человек на велосипеде может легко обогнать бегущего человека, хотя оба используют мускулы своих ног с равным усилием.
Определение работы как произведения силы на расстояние, на которое она действует, не говорит ничего относительно времени, которое требуется для того, чтобы выполнить данное действие. Люди обычно предпочитают выполнять какое-то количество работы за более короткое время, чем за длительное, и поэтому заинтересованы знать норму, по которой выполняется данная работа. Такая норма называется «мощностью». Единицы измерения мощности — Дж/с в системе МКС и эрг/с в системе СГС.
Очень распространенная единица мощности, которая не входит ни в какую систему, была разработана шотландским инженером Джеймсом Ваттом (1736–1819) в конце XVIII века, он улучшил паровой двигатель и сделал его пригодным для практического применения; он стремился узнать, насколько норма работы в водяной помпе его двигателя при откачке воды из угольных шахт отличается от нормы работы лошадей, которых до этого использовали в качестве силового привода на подобной работе. Чтобы определить «лошадиную силу», Ватт проверял, сколько веса, на какое расстояние и за какое время могут поднять лошади. Он пришел к заключению, что сильная лошадь могла поднять 150 фунтов веса на высоту 220 футов за одну минуту, так что одна лошадиная сила была равна 150?200/1, или 33 000 фунтов-футов в минуту.
Эта неудобная единица равна 745,2 Дж/с, или 7 452 000 000 эрг/с. Величине джоуль/секунда было в честь Джеймса Ватта присвоено название «ватт», так что мы можем также говорить, что одна лошадиная сила равна 745,2 ватта. Ватт, однако, наиболее часто используется при электрических измерениях. В механической инженерии (по крайней мере, в Великобритании и Соединенных Штатах) пока еще главенствует лошадиная сила. Например, мощность наших автомобильных двигателей обычно дается в лошадиных силах[27].
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК