Нейтрино

В гл. 11 мы говорили о том, что в ходе ядерных реакций масса переходит в энергию согласно формуле Эйнштейна e = тс². Это соответствие соблюдается и при полной аннигиляции частицы ее античастицей, и при образовании пары «частица — античастица» из энергии.

Несмотря на то что в большинстве случаев соотношение e = mc² выполняется полностью, в случае с радиоактивными излучениями существует одно исключение.

Альфа-излучение закону сохранения энергии подчиняется. Когда материнский атом самопроизвольно распадется на дочернее ядро и альфа-частицу, сумма образовавшихся продуктов отличается от массы исходного ядра. Это различие выражается в кинетической энергии быстрой альфа-частицы. Так как в результате распада ядра одного и того же элемента образуются одни и те же продукты, и разница в массе, и кинетическая энергия должны быть одинаковыми. Другими словами, пучок альфа-частиц должен быть моноэнергетическим, каковым он в данном случае и является.

У некоторых веществ испускаемый пучок альфа-частиц можно условно разделить на две и более группы, каждая из которых будет моноэнергетической, но уровень ее энергии будет отличаться от уровня энергии другой. Объясняется это тем, что материнское ядро может существовать на различных энергетических уровнях. В возбужденном состоянии ядро обладает несколько большей энергией, чем в обычном, и образующиеся при распаде такого ядра альфа-частицы обладают большей кинетической энергией. Каждому энергетическому уровню материнского ядра соответствует определенная группа моноэнергетических альфа-частиц, но соотношение массы и энергии остается неизменным (то есть соблюдается закон сохранения энергии).

Предполагалась, что все вышесказанное справедливо и для элементов, ядра которых распадаются на дочернее ядро и бета-частицу. Казалось вполне закономерным, что такие бета-частицы также образуют моноэнергетический пучок или в крайнем случае небольшую группу моноэнергетических лучей.

Однако в 1900 году Беккерель обнаружил, что разброс значений уровня кинетической энергии у излучаемых бета-частиц гораздо шире. В 1914 году Джеймс Чедвик доказал существование «непрерывного спектра бета-излучения».

Из потери массы была высчитана максимальная энергия бета-частицы, однако лишь у некоторых частиц уровень равнялся максимальному значению. (Ни у одной частицы уровень энергий не превышал максимальный, так как энергия, к сожалению, не образуется из ничего.)

Уровень энергии у бета-частиц был самым разнообразным (в пределах максимального). Некоторые вообще практически не обладали кинетической энергией. Более того, значительная часть энергии вообще куда-то исчезла, и в течение всех 1920-х годов ученые так и не могли обнаружить куда.

Исчезновение энергии так же невозможно, как и ее образование. Хотя некоторые физики, включая Нильса Бора, и готовы были признать закон сохранения энергии недействительным для субатомных частиц, остальные отчаянно искали какое-то другое объяснение.

В 1931 году Вольфганг Паули предложил свое объяснение. Он предположил, что во время образования бета-частицы образуется еще одна бета-частица, которая как раз и несет «недостающую» энергию первой бета-частицы.

В этом случае эта гипотетическая частица должна обладать определенными свойствами. При излучении бета-частицы сохраняется электрический заряд, то есть общий заряд образовавшихся частиц такой же, как и заряд исходных частиц. Соответственно частица Паули должна быть незаряженной. В этом был определенный смысл, так как если частица была бы заряженной, то во время своего движения она бы ионизировала окружающие атомы, то есть ее можно было бы обнаружить, например, в камере Вильсона. Но обнаружить ее не удалось.

Кроме того, обшей заряд предложенной Паули частицы был очень небольшим — равным недостающему количеству кинетической энергии электрона. От энергии частицы зависит ее масса, а значит, у частицы со столь низкой энергией и масса должна быть небольшой. Вскоре выяснилось, что масса новой частицы должна составлять менее 1% от массы электрона, то есть она уж точно являлась безмассовой.

Энрико Ферми, сразу заинтересовавшийся теорией Паули, хотел было дать название новой частице — «нейтрон», но к тому времени Чедвик уже обнаружил тяжелую незаряженную частицу, которую мы называем нейтроном. Тогда Ферми добавил к понравившемуся названию итальянский уменьшительно-ласкательный суффикс, и получился «нейтрино» («маленький и нейтральный»), и название прижилось.

Физики прозвали незаряженную безмассовую частицу «призраком», так как ее невозможно было обнаружить ни по заряду, ни по массе. Ее существование было бы очень сложно принять на веру, пусть даже и ради спасения закона сохранения энергии, если бы нейтрино не спасли еще три закона сохранения. 

Это стало очевидным после применения нейтрино к теории распада нейтронов. Нейтрон имеет период полураспада 12 мин и распадается на протон и электрон, причем кинетическая энергия вылетающего электрона может принимать различные значения. Тогда, по теории Паули, нейтрон распадается на три частицы: протон, электрон и нейтрино.

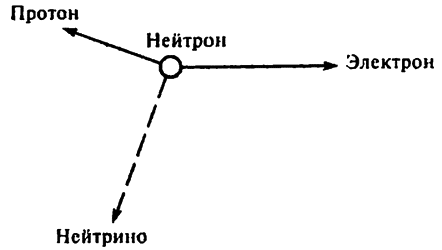
^{Распад нейтрона}

Разница между распадом до трех частиц вместо двух очень важна с связи с законом сохранения количества движения (см. ч. I). Если нейтрон в состоянии покоя распадается лишь на две частицы, они должны разлететься в противоположном друг от друга направлении по прямой траектории. Только в этом случае закон сохранения количества движения будет соблюден.

Если же этот нейтрон распадется на три частицы, то две из них вылетят по одну сторону от проведенной через центр ядра воображаемой прямой линии и их общий импульс будет компенсирован импульсом третьей частицы, вылетающей в противоположную сторону.

В результате проведенных исследований распада нейтрона выяснилось, что образующиеся протон и электрон вылетают по одну сторону от проведенной через центр ядра воображаемой прямой линии и что для сохранения количества движения просто необходимо существование третьей частицы, вылетающей по другую сторону от этой линии.

Как только удалось понять сущность спина частиц, стало ясно, что нейтрино очень удобно использовать и в связи с законом сохранения углового момента (см. ч. I). Спин нейтрона, протона и электрона может принимать значение +? либо –?. Предположим, что нейтрон распадется только на протон и электрон. Общий спин протона и электрона может быть равен +1, 0 или -1 (+? и +?, –? + ? или –? + –?). При любом раскладе общий их спин отличается от спина нейтрона (+? или –?), то есть угловой момент не сохраняется.

Теперь предположим, что спин нейтрино может быть равен +? или –?. Тогда общий спин трех частиц может быть равен +? или –?, например +?, +? и –?, то есть угловой момент сохраняется.

И наконец, третий, более тонкий закон сохранения. В предыдущей главе я говорил о законе сохранения барионного числа. Барионное число протона и нейтрона равно +1, а антипротона и антинейтрона –1. При распаде нейтрона барионное число сохраняется, так как из нейтрона (барионное число +1) образуется протон (барионное число +1).

А существует ли подобный закон для электронов, где число электрона будет равняться +1, а позитрона –1? Если мы рассматриваем только эти две частицы, то не будет. Например, в результате распада нейтрона образуется в том числе и один электрон, хотя в начале распада никаких электронов (или позитронов) нет.

Рассмотрим семейство электронов, включающее не только электроны и позитроны, но и нейтрино. Чтобы все сошлось, нам нужны еще и антинейтрино. Отличие антинейтрино от нейтрино заключается в направлении магнитного поля вращающейся частицы, как и в случае с нейтроном и антинейтроном (см. гл. 13). Электронное число нейтрино будет равно +1, а антинейтрино –1.

Теперь рассмотрим распад нейтрона с точки зрения вышесказанного. Электронное число нейтрона равно 0, так как он не является членом электронного семейства. Нейтрон распадается на протон (электронное число 0) и электрон (электронное число +1). Если добавить сюда и еще антинейтрино (электронное число –1) вместо нейтрино, то действует закон сохранения электронного числа (электронное число равно 0 до и после распада нейтрона).

Так же как и нейтрино, антинейтрино спасает законы сохранения энергии, количества движения и углового момента, а кроме того, добавляет еще один — закон сохранения электронного числа. Обозначив нейтрино как ?, а антинейтрино как ?^–, можем записать следующую формулу распада нейтрона:

n⁰ ? р⁺ + е^— + ?^–. (Уравнение 14.1)

С другой стороны, продуктом преобразования протона в нейтрон с испусканием позитрона (см. гл. 13) является частица с электронным числом –1. Для компенсации необходимо добавить еще и нейтрино (электронное число — 1). Запишем это:

p⁺ ? n⁰ + е⁺ + ?⁰. (Уравнение 14.2)

И действительно, допуская образование в ходе ядерных реакций нейтрино и антинейтрино, мы можем сохранить соблюдение четырех законов сохранения: энергии, количества движения, углового момента и электронного числа. Ради получения этой «компенсации в четырехкратном размере» придется признать существование нейтрино и антинейтрино независимо от того, можно их обнаружить или нельзя.