Атом Бора

Итак, электроны атома водорода не только не падают на ядро, но еще и испускают волны определенной частоты, которые можно определить по простым формулам Ридберга. Нужна была новая модель атома, которая бы все это отражала.

Такую модель создал в 1913 году датский физик Нильс Бор (1885–1962). Он предложил использовать для решения задачи только в то время появившуюся квантовую теорию (см. ч. II).

Согласно квантовой теории, любой преобразовывающий кинетическую энергию в излучение объект теряет эту энергию. Так, например, Земля постепенно теряет кинетическую энергию за счет вращения вокруг Солнца, однако эти потери настолько малы, что даже самые точные измерения не смогут зафиксировать какое-либо изменение в скорости вращения планеты.

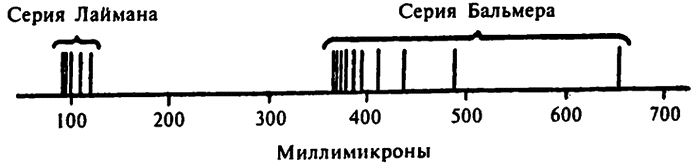
^{Спектр водорода} 

Но с электронами дело обстоит иначе. Общая кинетическая энергия электрона немного превышает энергию одного кванта видимого света, то есть для излучения одного кванта света электрону потребуется мгновенно потратить всю свою энергию. Однако вместо того, чтобы медленно приближаться к ядру во время вращения (как это себе представляли физики «доквантовой» эры), электрон просто «перепрыгнет» на более близкую к ядру орбиту. С другой стороны, если электрон также еще и поглощает свет, значит, он сразу поглотит целый квант света и на этот раз перепрыгнет уже на более высокую орбиту.

Бор предположил, что электрон в основном состоянии обладает минимумом энергии и находится на ближайшей к ядру орбите. Такой электрон не выделяет энергию (истинная причина этого открылась лишь 10 лет спустя, см. гл. 6). После поглощения энергии электрон переходит в возбужденное состояние и в зависимости от количества этой энергии занимает одну из более удаленных от ядра орбит.

Бор определил несколько орбит электрона в атоме водорода в зависимости от величины кинетического момента. Используя постоянную Планка (см. ч. II), Бор вывел следующую формулу:

p = nh/2? , (Уравнение 5.9)

где p — кинетический момент электрона, h — постоянная Планка, ? — это конечно же известная нам постоянная длины окружности; n — любое положительное целое. Теперь введем в формулу значение постоянной Планка, предположим, что электрон может двигаться только по определенным орбитам, примем за n любое целое число и получим квантованный атом.

В связанных с квантованным атомом вычислениях выражение h/2? используется часто, поэтому его обычно сокращают до ?. Так как значение h приблизительно 6,6256?10^–27 эрг-с, значение ? приблизительно 3,14159, то ? приблизительно равно 1,0545?10^–27 эрг-с.

Таким образом, формула 5.9 приобретает вид:

p = n (1,0545?10^–27). (Уравнение 5.10)

Иногда n называют еще главным квантовым числом (кроме главного, существуют и другие квантовые числа). Это число обозначает орбиту, на которой находится электрон: n = 1 для ближайшей к ядру орбите; 2, 3, 4 и так далее — для более высоких.

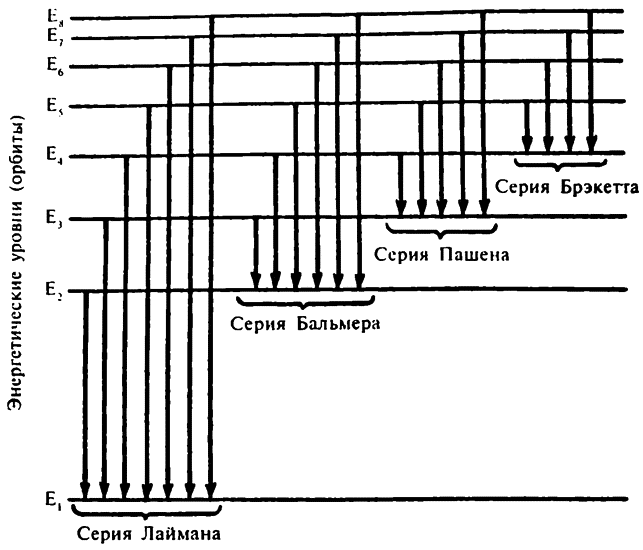
Когда единственный электрон атома водорода опускается с орбиты 2 на орбиту 1, он выделяет один квант (определенного размера) энергии, т. е. излучение определенной частоты, и в определенном месте спектра появится яркая линия. (А когда единственный электрон атома водорода поднимается с орбиты 1 на орбиту 2, он поглощает один квант (того же определенного размера), и на месте яркой спектральной линии появится еще и темная.)

Если единственный электрон атома водорода опустится с орбиты 3 на орбиту 1, то энергии при этом выделится больше, и частота излучаемого света будет выше. При перемещении с орбиты 3 (4, 5) на орбиту 1 частота будет еще выше.

Серия перемещений с различных орбит на орбиту 1 приведет к излучению света последовательно повышающейся частоты (или последовательно понижающейся длины волны), то есть серии волн Лаймана. Серия перемещений с более высоких орбит на орбиту 2 приведет к появлению серии Бальмера, на орбиту 3 — серии Пашена и т. д.

В описывающих длины волн спектральных линий различных серий формулах (5.5, 5.6, 5.7, 5.8) первое число знаменателя правой части и будет главным квантовым числом орбиты, куда опускается (или с которой поднимается) электрон.

Заряд ядра атомов более сложной, чем у водорода, структуры с несколькими электронами больше, следовательно, электроны на внутренней орбите удерживаются сильнее.

Поэтому для перемещения на более высокую орбиту электрону требуется больше энергии, а значит, и при переходе на более низкую орбиту энергии также освобождается больше. Самые короткие излучаемые водородом волны находятся в ультрафиолетовой части спектра (серия Лаймана), а более сложные атомы могут излучать и сверхкороткие рентгеновские лучи. Мозель обнаружил, что длина волн рентгеновского излучения уменьшается с возрастанием атомного числа элемента.

Дальше — хуже. Модель атома Бора вполне подходила для атомов водорода, чей спектр состоит из прямых линий. Однако более точный спектральный анализ показал, что спектральные линии водорода имеют тонкую структуру, состоящую из многих мелких линий, будто электрон при перемещении на другую орбиту «промахивается» и попадает на соседнюю.

^{Атом Бора} 

Это едва не поставило крест на квантовой модели атома. Положение спас в 1916 году немецкий физик Арнольд Зоммерфельд (1868–1951), предложивший следующее объяснение: дело в том, что, по мнению Бора, электронные орбиты имели четкую форму круга, однако Зоммерфельд предположил, что она может быть и эллиптической. Квантовая модель атома допускала существование орбит с небольшим эксцентриситетом эллипса, а главное квантовое число — группы орбит, состоящих из одной круговой и нескольких эллиптических, так как изменения кинетического момента были незначительными.

Для эллиптических орбит Зоммерфельд ввел понятие орбитального квантового числа, получившего обозначение L[125]. Орбитальное квантовое число может принимать любое значение в пределах от 0 до n – 1, то есть при n = 1 L = 0; при n = 2 L = 0 или 1; при n = 3 L = 0, 1 или 2 и т. д.

Но спектральные линии под действием магнитного поля расходятся еще больше. Ученые приняли это во внимание и ввели магнитное квантовое число (m).

С появлением магнитного атомного числа атом стали рассматривать уже в трех измерениях. Теперь варьировалась не только форма орбиты электрона, но и ее наклон относительно основной. Для т справедливы все значения L, кроме того, к положительным значениям добавились еще и отрицательные. То есть если для n = 2 L = 1 или 0, а m = 0, 1 и –1; для n = 3 L = 0, 1 или 2, а m = 0, 1, 2, –1 или –2 и т. д.

Последнее квантовое число — число спина электрона (s). Оно обозначает спин, т. е. направление вращения электрона вокруг своей оси, а поскольку таких направлений всего два — по часовой стрелке и против часовой, то и квантовое число может принимать лишь два значения: 1/2 и –1/2.