Материальные волны

Попытка Бора применить квантовую теорию к атому принесла огромное количество как теоретических, так и практических плодов: удалось дать объяснение периодической таблице, появился совершенно новый класс устройств — твердотельные приборы… Физики остались довольны.

Но квантованный атом не решил проблем химиков, так и не объяснив, как же атомы соединяются в молекулы. Если модель атома Льюиса — Ленгмюра хоть как-то объясняла этот процесс с помощью кубов и общих электронов, то разобрать что-либо среди прыгающих с одного энергетического уровня на другой электронов квантованного атома было просто невозможно.

Ответ вырос из другой неразрешимой на первый взгляд загадки — связи между частицами и волнами. В начале XX века физики окончательно убедились, что свойства света да и электромагнитных волн в целом точно такие же, как и у частиц. Комптон-эффект (см. ч. II) окончательно убедил ученых, что частицы и волны могут образовывать единое целое и совмещать в себе свойства и частиц, и волн.

Но относится ли это лишь к электромагнитному излучению? Что, если не только волны проявляют свойства частиц, но частицы также могут проявлять некоторые свойства волн?

Французский физик Луи де Бройль (1892–1987) как раз занимался изучением этого вопроса. Он применил к электронам соотношения, справедливые для фотонов, то есть частиц. В 1923 году де Бройль опубликовал следующую формулу:

? = h/mv, (Уравнение 6.1)

где h — постоянная Планка (см. ч. II); m — масса движущейся частицы; v — ее скорость (произведение mv есть ее импульс); ? — принятое обозначение длины волны.

Теоретически эту формулу можно применить к любому движущемуся объекту, хоть к теннисному мячу, хоть к планете. Однако с возрастанием импульса длина волны сокращается, поэтому измерить частоту излучения, испускаемого летящим теннисным мячом, существующими способами просто невозможно, да и не нужно.

Тем не менее длина волн, излучаемых объектами с ничтожной массой, например электронами, относительно велика и равняется длине волны рентгеновского луча. (Впрочем, хотя длина волны и одинаковая, природа такого излучения отличается от природы рентгеновского луча. Волны, излучаемые частицами, по своей природе не являются электромагнитными, поэтому мы назовем их «материальными волнами».)

Если длина материальной волны равна длине волны рентгеновского излучения, значит, ее можно обнаружить тем же способом, что и рентгеновский луч. Рентгеновское излучение было обнаружено при помощи кристаллов. Так, может, и материальные волны можно также обнаружить при помощи кристаллов?

Первые удачные попытки осуществить это были сделаны в 1927 году английским физиком Джорджем Томсоном (1892–1975), а также американскими физиками Клинтоном Дэвиссоном (1881–1958) и Лестером Гермером (1896–1971), работавшими независимо от Томсона. В последующие годы ученым удалось обнаружить волновые свойства и у других, более тяжелых частиц, и уже не осталось никаких сомнений в том, что любой объект, обладающий волновыми свойствами, обладает и свойствами частицы, и наоборот.

Аналогия между материальными волнами и электромагнитным излучением проявилась в микроскопии.

При использовании световых волн у микроскопа существует предел разрешающей способности, и, какой совершенной бы ни была оптическая «начинка» прибора, с его помощью нельзя изучать образцы, размеры которых меньше ³/₅ длины световой волны.

Образно говоря, свет будет просто «обходить» такой образец. Даже при использовании самых коротких видимых световых волн, скажем длиной 380 миллимикрон, с помощью микроскопа невозможно будет разглядеть объекты менее 200 миллимикрон в диаметре, например вирусы. Таким образом, оптический микроскоп позволяет увеличивать изображение максимум в 2000 раз.

Для увеличения разрешающей способности микроскопов сначала стали применять электромагнитные волны, но использование материальных волн дало максимальный результат. Сегодня для этих целей используются в основном электронные волны, длина которых равна длине рентгеновского излучения. С помощью магнитного поля можно сфокусировать четкий электронный пучок так же, как можно сфокусировать пучок света с помощью линзы. Образец должен быть довольно тонким, чтобы электроны могли свободно проходить сквозь него. Кроме того, образец должен находиться в вакууме, иначе содержащиеся в воздухе частицы рассеют электронный пучок. С помощью такого микроскопа можно исследовать абсолютное большинство предметов.

Образец располагается между источником электронного излучения и фотографической пластиной или же люминесцентным экраном. Проходя через образец, электроны рассеиваются и поглощаются отдельными его частями, в результате чего на экране появляется черно-белое изображение объекта.

Первый электронный микроскоп был создан в 1931 году в Германии немецким физиком Эрнстом Руской (1906–1988). Уже в 1934 году были созданы электронные микроскопы, превосходящие по увеличению оптические, а начинам с 1939 года такие микроскопы стали производить в коммерческих целях. Современные электронные микроскопы увеличивают в тысячи крат сильнее, чем лучшие их оптические собратья.

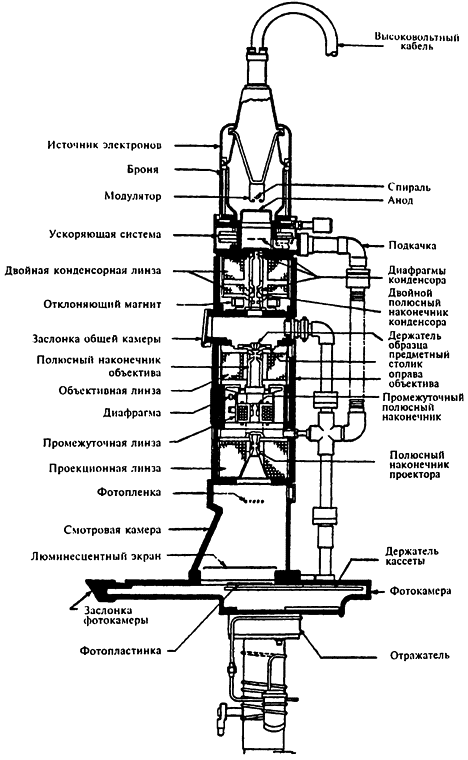
^{Электронный микроскоп} 

Материальные волны вошли и в мир атомной теории. Австрийский физик Эрвин Шрёдингер (1887–1961) подошел к проблеме изучения структуры атома с точки зрения не только частиц, но и волн.

Шрёдингер представил электрон в виде вращающейся вокруг ядра волны. В этом случае описываемая электроном орбита должна соответствовать количеству испускаемых электроном волн. За один оборот вокруг ядра по постоянной орбите электрон излучает одно и то же количество волн, т. е. его излучение является стоячей волной.

Когда электрон поглощает некоторое количество энергии, длина его волны уменьшается, и, оставаясь на той же орбите, он уже не может излучать такое же количество волн. То же самое происходит и когда электрон теряет часть своей энергии, а длина волны увеличивается.

Учитывая, что количество волн, производимых электроном за один оборот вокруг ядра, не должно быть дробным числом, необходимо, чтобы при излучении или поглощении электроном энергии длина испускаемых волн увеличивалась или уменьшалась, а их общее количество оставалось целым числом. Например, если вместо четырех волн электрон будет излучать пять более коротких, то уровень его энергии увеличится, а если вместо четырех волн будет три более длинных — уменьшится. Если количество испускаемых волн сократилось до одной волны максимальной длины, значит, электрон опустился на ближайший к ядру энергетический уровень и больше не может терять энергию.

Получается, что каждому энергетическому уровню соответствует определенная стоячая волна. Шрёдингер проанализировал все это математически и в 1926 году вывел волновое уравнение.

Изучение поведения атомов на основе модели Шрёдингера называется волновой механикой, или, так как поглощаться или излучаться могут лишь кванты энергии, квантовой механикой.

Квантовая механика тут же завладела сердцами физиков. Она превосходила матричную механику Гейзенберга (см. гл. 6) психологически, так как квантовая механика Шрёдингера давала волнам визуальный облик, пусть и сложный для восприятия, в то время как числам Гейзенберга явно не хватало наглядности.

В 1944 году венгерский математик Джон Нейман (1903–1957) выдвинул предположение, что с математической точки зрения квантовая механика и матричная механика равнозначны: одно и то же явление можно продемонстрировать с точки зрения как квантовой, так и матричной механики[126].

Теоретически квантовую теорию можно применить и для объяснения химического поведения атомов. Однако, как показывает практика, произвести подобные чудовищные расчеты невозможно даже с использованием современных вычислительных средств. Поэтому химия до сих пор остается намного менее изученной наукой, чем физика.

Тем не менее с помощью квантовой теории можно объяснить процесс формирования молекул из атомов. Американский химик Лайнус Полинг (1901–1994) показал, как из двух атомов образуется молекула — соединение, обладающее гораздо большей, чем отдельные атомы, стабильностью. Общая электронная оболочка модели атома Льюиса — Ленгмюра у Полинга превратилась в две резонирующих друг с другом волны (см. ч. I). Теория резонанса Полинга подробно описана в его работе «Природа химических связей» (1939).

Теория резонанса объясняет структуру и поведение молекул гораздо глубже, чем модель Льюиса — Ленгмюра. В частности, Полингу удалось объяснить образование молекул бензола и гидридов бора. Вообще квантовая механика помогает разгадывать все больше и больше тайн современной химии.

В 1927 году Гейзенберг выявил еще одно важное свойство волновой природы электрона (и частиц в целом). Дело в том, что если рассматривать частицу не как частицу, а как волну, то картинка получается гораздо более размытой. А так как все во Вселенной состоит из частиц, обладающих в том числе и свойствами волн, то и картина Вселенной также становится гораздо более размытой.

Местоположение любой частицы (или ее центра) в космосе можно определить с очень большой точностью, а вот точное местоположение волны определить уже гораздо сложнее.

Рассуждая над этим, Гейзенберг предположил, что невозможно одновременно точно определить и местоположение, и импульс частицы. Доводом ученого являлось то, что любая попытка точно определить местоположение частицы (любым технически возможным и невозможным способом) автоматически приводит к изменению скорости движения этой частицы и соответственно к изменению ее импульса, т. е. значение ее импульса станет более неопределенным. И наоборот, любая попытка точно измерить импульс частицы приведет к изменению ее местоположения, и местоположение будет более неопределенным. Чем выше точность измерения одной величины, тем выше погрешность изменения второй.

Кратко вышесказанное можно выразить следующей формулой:

(?p)(?x) = h, (Уравнение 6.2)

где ?p — погрешность измерения местоположения, ?x — погрешность измерения импульса; h — постоянная Планка (символ ? означает «приблизительно равно»). Эта формула получила название принцип неопределенности Гейзенберга.

С философской точки зрения Гейзенберг пришел к весьма неутешительным выводам, ведь еще со времен Ньютона ученые свято верили в науку, верили в то, что хотя бы теоретически измерения можно производить с абсолютной точностью. А тут выясняется, что на пути к абсолютному знанию стоит непреодолимая стена, стена, возведенная самим мирозданием. Конечно, это тяжелый удар для всего научного сообщества.

Даже сам Эйнштейн долго не мог примириться с неопределенностью, так как этот принцип ставил под сомнение существование причинно-следственных связей на субатомном уровне. Получается, что все в мире происходит случайно. Раз невозможно определить точное местоположение электрона, то как тогда подсчитать силу вероятного воздействия на него извне? «Я не могу поверить, — говорил Эйнштейн, — что Господь Бог играет со всем миром в кости».

И тем не менее Эйнштейну не удалось найти в принципе неопределенности каких-либо противоречий, а современная физика эту теорию полностью приняла.

Однако особых поводов для печали нет. Постоянная Планка очень мала, поэтому значением относительной неопределенности для тел, чьи размеры превышают размеры атома, можно пренебречь. Так что принцип неопределенности правит бал только лишь в субатомном мире.

Более того, принцип неопределенности вовсе не нанес науке никакого оскорбления. Даже наоборот, если во Вселенной существует пусть и очень малая, но приводящая к критическим последствиям доля неопределенности, следует отдать ученым дань за то, что они смогли ее обнаружить. Конечно же осознание пределов своего знания уже само по себе знание первостепенной важности.