§ 7. Поля без роторов и поля без дивергенций

Теперь перейдем к некоторым следствиям из наших новых теорем. Возьмем сперва случай вектора, у которого ротор (или вихрь) повсюду равен нулю. Тогда, согласно теореме Стокса, циркуляция по любому контуру — нуль. Если мы теперь возьмем две точки (1) и (2) на замкнутой кривой (фиг. 3.12), то криволинейный интеграл от касательной составляющей от (1) до (2) не должен зависеть от того, какой из двух возможных путей мы выбрали.

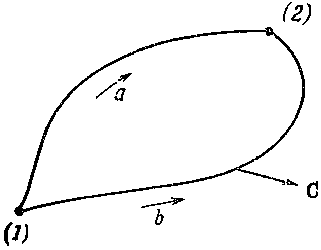
Фиг. 3.12. Если ??С равно нулю, то циркуляция по замкнутой привой ? тоже нуль. Криволинейный интеграл от C·ds на участке от (1) до (2) вдоль а должен быть равен интегралу вдоль b.

Можно заключить, что интеграл от (1) до (2) может зависеть только от расположения этих точек, т. е. что он есть функция только от координат точек. Той же логикой мы пользовались в вып. 1, гл. 14, когда доказывали, что если интеграл от некоторой величины по произвольному замкнутому контуру всегда равен нулю, то этот интеграл может быть представлен в виде разности функций от координат двух концов. Это позволило нам изобрести понятие потенциала. Мы доказали далее, что векторное поле является градиентом этой потенциальной функции [см. вып. 1, уравнение (14.13)].

Отсюда следует, что любое векторное поле, у которого ротор равен нулю, может быть представлено в виде градиента некоторой скалярной функции, т. е. если ??C=0 всюду, то существует некоторая функция ? (пси), для которой С=?? (полезное представление). Значит, мы можем, если захотим, описывать этот род векторных полей при помощи скалярных полей.

Теперь докажем еще одну формулу. Пусть у нас есть произвольное скалярное поле ? (фи). Если взять его градиент ??, то интеграл от этого вектора по любому замкнутому контуру должен быть равен нулю. Криволинейный интеграл от точки (1) до точки (2) равен [?(2)-?(1)]. Если точки (1) и (2) совпадают, то наша теорема 1 [уравнение (3.8)] сообщает нам, что криволинейный интеграл равен нулю:

Применяя теорему Стокса, можно заключить, что

по любой поверхности. Но раз интеграл по любой поверхности равен нулю, то подынтегральное выражение обязано быть равно нулю. Значит,

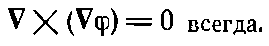
Тот же результат был доказан в гл. 2, § 7 при помощи векторной алгебры.

Рассмотрим теперь частный случай, когда на маленький контур ? натягивается большая поверхность S (фиг. 3.13).

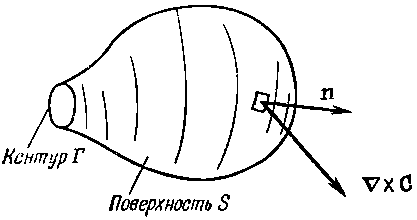
Фиг. 3.13. При переходе к пределу замкнутой поверхности поверхностный интеграл от (??С)_n должен обратиться в нуль.

Мы хотим посмотреть, что случится, когда контур стянется в точку. Тогда граница поверхности исчезнет, а сама поверхность превратится в замкнутую. Если вектор С повсюду конечен, то криволинейный интеграл по ? должен стремиться к нулю по мере стягивания контура (интеграл в общем-то пропорционален длине контура ?, а она убывает). Согласно теореме Стокса, поверхностный интеграл от (??С)_n тоже должен убывать до нуля. Когда поверхность замыкается, то при этом каким-то образом в интеграл привносится вклад, который взаимно уничтожается с накопленным ранее. Получается новая теорема:

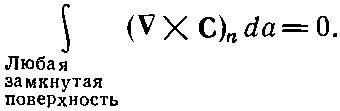
Это нас должно заинтересовать, потому что у нас уже есть одна теорема о поверхностном интеграле векторного поля. Такой поверхностный интеграл равен объемному интегралу от дивергенции вектора, как это следует из теоремы Гаусса [уравнение (3.18)]. Теорема Гаусса в применении к ??С утверждает, что

(3.40)

Мы заключаем, что интеграл в правой части должен обращаться в нуль

(3.41)

и что это должно быть справедливо для любого векторного поля С, каким бы оно ни было. Раз уравнение (3.41) выполнено для произвольного объема, то в каждой точке пространства подынтегральное выражение должно быть равно нулю. Получается, что

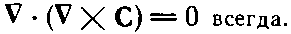
Тот же результат был выведен с помощью векторной алгебры в гл. 2, § 7. Теперь мы начинаем понимать, как все здесь прилажено одно к другому.