§ 6. Потенциалы заряда, движущегося с постоянной скоростью; формула Лоренца

Применим теперь потенциалы Льенара-Вихерта к случаю заряда, движущегося по прямой с постоянной скоростью, и вычислим поле этого заряда. Позже мы повторим этот вывод, используя уже принцип относительности. Мы знаем величину потенциалов в той системе, в которой заряд покоится. Когда заряд движется, то все получается простым релятивистским преобразованием от одной системы к другой. Но теория относительности ведет свое начало от теории электричества и магнетизма. Формулы преобразований Лоренца [см. гл. 15 (вып. 2)]— это открытия, сделанные Лоренцем при исследовании уравнений электричества и магнетизма. И для того чтобы вы понимали, откуда все пошло, я хочу показать вам, что уравнения Максвелла действительно приводят к преобразованиям Лоренца. Я начну с вычисления потенциала равномерно движущегося заряда прямо из электродинамики, из уравнений Максвелла. Мы уже показали, что уравнения Максвелла приводят к потенциалу, полученному в предыдущем параграфе. Стало быть, пользуясь этими потенциалами, мы используем тем самым теорию Максвелла.

Пусть имеется заряд, движущийся вдоль оси х со скоростью v (фиг. 21.8).

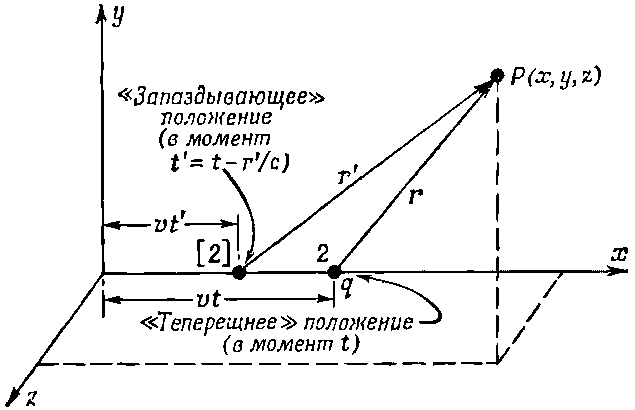
Фиг. 21.8. Определение потенциала в точке Р заряда, движущегося равномерно вдоль оси х.

Нас интересуют потенциалы в точке Р(х, у, z). Если t=0 — момент, в который заряд проходит через начало координат, то в момент t заряд окажется в точке x=vt, y=z=0. А нам нужно знать его положение с учетом запаздывания, т. е. положение в момент

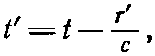(21.35)

где r' — расстояние от заряда до точки Р в этот запаздывающий момент. В это более раннее время t' заряд был в x=vt', так что

(21.36)

Чтобы найти r' или t', это уравнение надо сопоставить с (21.35). Исключим сперва r', решив (21.35) относительно r' и подставив в (21.36). Возвысив затем обе части в квадрат, получим

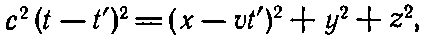
т. е. квадратное уравнение относительно t'. Раскрыв скобки и расположив члены по степеням t', получим

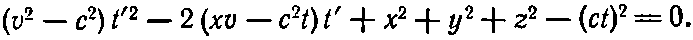
Отсюда найдем

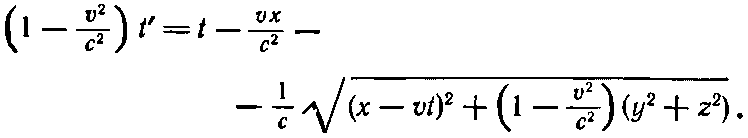(21.37)

Чтобы получить r', надо это t' подставить в

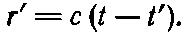
Теперь мы уже можем найти ? из выражения (21.33), имеющего вид

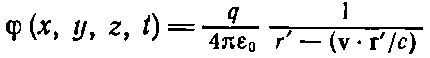(21.38)

(ввиду того, что v постоянно).

Составляющая v в направлении r' равна v(x-vt')/r', так что v·r' просто равно v(x-vt'), а весь знаменатель равен

Подставляя (1-v²/c²)t' из (21.37), получаем

Это уравнение становится более понятным, если переписать его в виде

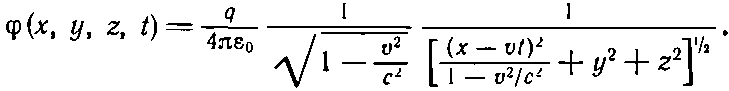(21.39)

Векторный потенциал А — это такое же выражение, но с добавочным множителем v/c²:

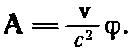
В выражении (21.39) со всей ясностью предстает перед вами начало преобразований Лоренца. Если бы заряд находился в начале координат в своей собственной системе покоя, то его потенциал имел бы вид

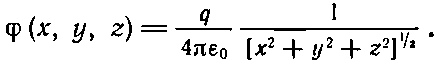
А мы смотрим на него из движущейся системы координат, и нам кажется, что координаты следует преобразовать с помощью формул

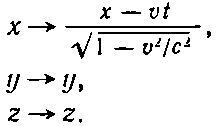
Это обычное преобразование Лоренца. Лоренц вывел его тем же самым способом, каким пользовались и мы.

Но что можно сказать о добавочном множителе 1/?(1-v²/с²), который появился перед дробью в (21.39)? И кроме того, как появляется векторный потенциал А, если он в системе покоя частицы повсюду равен нулю? Мы вскоре покажем, что А и ? вместе составляют четырехвектор, подобно импульсу р и полной энергии U частицы. Добавка 1/?(1—v²/c²) в (21.39)—это тот самый множитель, который появляется всегда, когда преобразуют компоненты четырехвектора, так же как плотность заряда ? преобразуется в ?/?(1-v²/c²). Собственно из формул (21.4) и (21.5) почти очевидно, что А и ? суть компоненты одного четырехвектора, потому что в гл. 13 (вып. 5) уже было показано, что j и ? — компоненты четырехвектора.

Позднее мы более подробно разберем относительность в электродинамике; здесь мы хотели только показать, как естественно уравнения Максвелла приводят к преобразованиям Лоренца. Поэтому не надо удивляться, узнав, что законы электричества и магнетизма уже вполне пригодны и для теории относительности Эйнштейна. Их не нужно даже как-то особо подгонять, как это приходилось делать с ньютоновой механикой.