§ 3. Общее решение уравнений Максвелла
Мы нашли решение уравнения (21.7) для «точечного» источника. Теперь встает новый вопрос: Каков вид решения для рассредоточенного источника? Ну, это решить легко; всякий источник s(x, у, z, t) можно считать состоящим из суммы многих «точечных» источников, расположенных поодиночке в каждом элементе объема dV и имеющих силу s(x, у, z, t)dV. Поскольку (21.7) линейно, суммарное поле представляет собой суперпозицию полей от всех таких элементов источника.
Используя результаты предыдущего параграфа [см. (21.13)], мы получим, что в момент t поле d? в точке (х1, y1, z1) [или, короче, в точке (1)], создаваемое элементом источника sdV в точке (х2, у2, z2) [или, короче, в точке (2)], выражается формулой

где r12 — расстояние от (2) до (1). Сложение вкладов от всех частей источника означает, конечно, интегрирование по всей области, где s?0, так что мы имеем
 (21.14)
(21.14)
Иначе говоря, поле в точке (1) в момент времени t представляет собой сумму всех сферических волн, испускаемых в момент t-r12/c всеми элементами источника, расположенного в точке (2). Выражение (21.14) является решением нашего волнового уравнения для любой системы источников.
Теперь мы видим, как получать общее решение уравнений Максвелла. Если подразумевать под ? скалярный потенциал ?, то функция источника s превращается в ?/?0. А можно считать, что ? представляет одну из трех компонент векторного потенциала А; тогда s означает соответствующую компоненту j/?0c2. Стало быть, если во всех точках известна плотность зарядов ?(х, у, z, t) и плотность тока j(х, у, z, t), то решения уравнений (21.4) и (21.5) можно выписать немедленно:
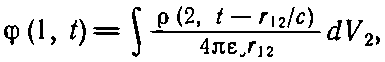 (21.15)
(21.15)
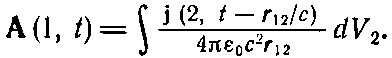 (21.16)
(21.16)
Поля Е и В получатся дифференцированием потенциалов [используются выражения (21.2) и (21.3)]. Кстати, можно проверить явно, что ? и А, полученные из (21.15) и (21.16), действительно удовлетворяют равенству (21.6).
Мы решили уравнения Максвелла. В любых обстоятельствах, если только заданы токи и заряды, из этих интегралов можно определить потенциалы, а затем, продифференцировав их, получить поля. Тем самым с теорией Максвелла покончено. И это позволяет нам также замкнуть круг и вернуться к нашей теории света, потому что достаточно только подсчитать электрическое поле движущегося заряда, чтобы связать все это с нашей прежней теорией света. Все, что нам остается сделать,— это взять движущийся заряд, вычислить из этих интегралов его потенциал и затем из -??-?A/?t, дифференцируя, найти Е. Мы должны получить формулу (21.1). Работы придется проделать много, но принцип ясен.
Итак, мы дошли до центра электромагнитной вселенной. У нас в руках полная теория электричества, магнетизма и света, полное описание полей, создаваемых движущимися зарядами, и многое, многое другое. Все сооружение, воздвигнутое Максвеллом, во всей его полноте, красе и мощи сейчас перед нами. Это, пожалуй, одно из величайших свершений физики. И чтобы напомнить о его важности, мы переписываем все формулы вместе и обводим их красивой рамкой.
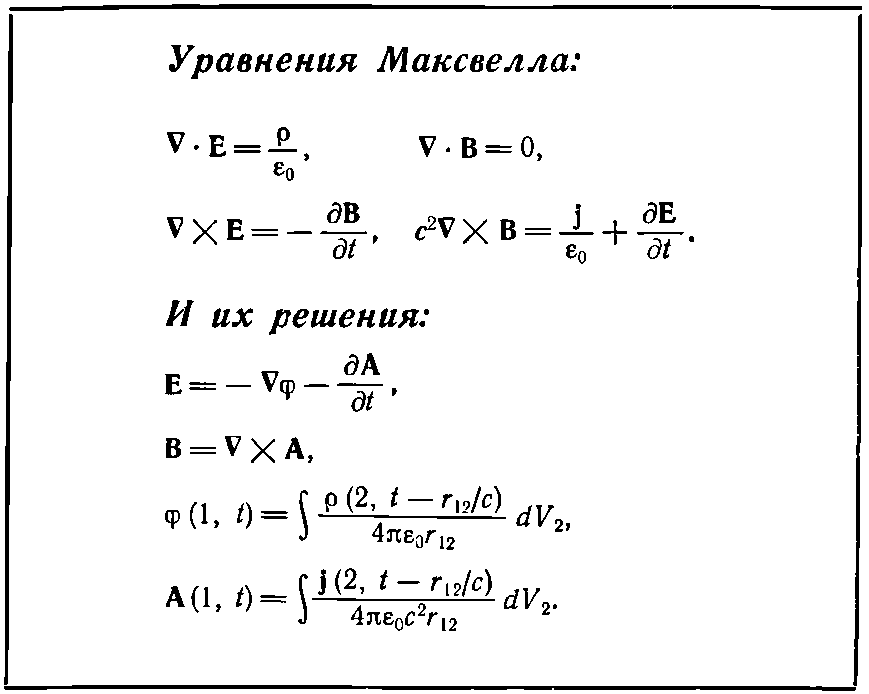
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК