§ 5. Четырехмерный потенциал движущегося заряда

Теперь выпишем законы преобразования, выражающие ? и А в движущейся системе через ? и А в неподвижной, хотя неявно мы уже говорили о них. Поскольку А_?=(?, А) является четырехвектором, это уравнение должно выглядеть подобно (25.1), за исключением того, что t нужно заменить на ?, а x — на А. Таким образом,

(25.24)

При этом предполагается, что штрихованная система координат движется по отношению к нештрихованной со скоростью v в направлении оси х.

Рассмотрим один пример плодотворности идеи 4-потенциала. Чему равны векторный и скалярный потенциалы заряда q, движущегося со скоростью v в направлении оси х? Задача очень упрощается в системе координат, движущейся вместе с зарядом, ибо в этой системе заряд покоится. Пусть заряд находится в начале координат системы S', как это показано на фиг. 25.2.

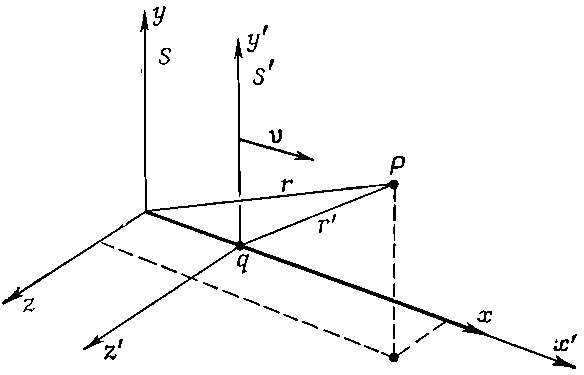
Фиг. 25.2. Система отсчета S' движется со скоростью v (в направлении оси х) по отношению к системе S. Заряд, покоящийся в начале системы координат S', находится в системе S в точке x=vt. Потенциалы в точке Р могут быть найдены для любой системы отсчета.

Скалярный потенциал в движущейся системе задается выражением

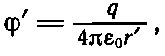(25.25)

причем r' — расстояние от заряда q до точки в движущейся системе, где производится измерение поля. Векторный же потенциал А', разумеется, равен нулю.

Теперь без особых хитростей можно найти потенциалы ? и А в неподвижной системе координат. Соотношениями, обратными к уравнениям (25.24), будут

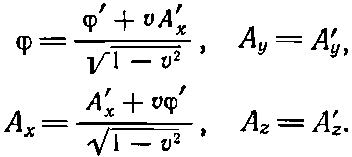(25.26)

Используя далее выражение для ?'[см. (25.25)] и равенство А'=0, получаем

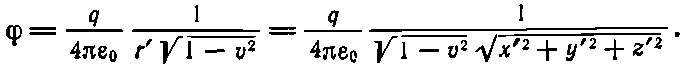
Эта формула дает нам скалярный потенциал ?, который мы увидели бы в системе S, но он, к сожалению, записан через координаты штрихованной системы. Впрочем, это дело легко поправимо; с помощью (25.1) можно выразить t', х', у', z' через t, x, у, z и получить

(25.27)

Повторяя ту же процедуру для вектора А, вы можете показать, что

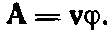(25.28)

Это те же самые формулы, которые мы вывели в гл. 21, но там они были получены другим методом.