§ 8. Линии поля; эквипотенциальные поверхности
Теперь мы собираемся дать геометрическое описание электростатического поля. Два закона электростатики: один — о пропорциональности потока и внутреннего заряда и другой — о том, что электрическое поле есть градиент потенциала, могут также быть изображены геометрически. Мы проиллюстрируем это двумя примерами.
Первый пример: возьмем поле точечного заряда. Проведем линии в направлении поля, которые повсюду касательны к векторам поля (фиг. 4.12).
Фиг. 4.12. Линии поля и эквипотенциальные поверхности для положительного точечного заряда.
Их называют линиями поля. Линии поля всюду показывают направление электрического вектора. Но, кроме этого, мы хотим изобразить и абсолютную величину вектора. Можно ввести такое правило: пусть напряженность электрического поля представляется «плотностью» линий. Под этим мы подразумеваем число линий на единицу площади, перпендикулярной линиям. С помощью этих двух правил мы можем начертить картину электрического поля. Для точечного заряда плотность линий должна убывать как 1/r2. Но площадь сферической поверхности, перпендикулярной к линиям на всех радиусах r, возрастает как r2, так что если мы сохраним всюду, на всех расстояниях от центра, одно и то же число линий, то их плотность останется пропорциональной величине поля. Мы можем гарантировать неизменность числа линий на всех расстояниях, если обеспечим непрерывность линий, т. е. если уж линия вышла из заряда, то она никогда не кончится. На языке линий поля закон Гаусса утверждает, что линии могут начинаться только в плюс-зарядах и кончаться только в минус-зарядах. А число линий, покидающих заряд q, должно быть равно q/?0.
Сходную геометрическую картину можно отыскать и для потенциала ?. Проще всего изображать его, рисуя поверхности, на которых ? постоянно. Их называют эквипотенциальными, т. е. поверхностями одинакового потенциала. Какова геометрическая связь эквипотенциальных поверхностей и линий поля? Электрическое поле является градиентом потенциала. Градиент направлен по самому быстрому изменению потенциала, поэтому он перпендикулярен к эквипотенциальной поверхности. Если бы Е не было перпендикулярно к поверхности, у него существовала бы составляющая вдоль поверхности и потенциал изменялся бы вдоль поверхности и тогда нельзя было бы считать ее эквипотенциальной. Эквипотенциальные поверхности должны поэтому непременно всюду проходить поперек линий электрического поля.
У отдельно взятого точечного заряда эквипотенциальные поверхности — это сферы с зарядом в центре. На фиг. 4.12 показано пересечение этих сфер с плоскостью, проведенной через заряд.
В качестве второго примера рассмотрим поле близ двух одинаковых зарядов, одного положительного, а другого отрицательного. Это поле получить легко. Это суперпозиция (наложение) полей каждого из зарядов. Значит, мы можем взять две картинки, похожие на фиг. 4.12, и наложить их... нет, это невозможно! Тогда получились бы пересекающиеся линии поля, а этого быть не может, потому что Е не может иметь в одной точке двух направлений. Неудобство картины линий поля теперь становится очевидным. С помощью геометрических рассуждений невозможно в простой форме проанализировать, куда пойдут новые линии. Из двух независимых картин нельзя получить их сочетание. Принцип наложения, столь простой и глубокий принцип теории электрических полей, в картине полевых линий не имеет простого соответствия.
Картина полевых линий все же имеет свою область применимости, так что мы можем все же захотеть начертить эту картину для пары равных (и противоположных) зарядов. Если мы вычислим поля из уравнения (4.13), а потенциалы из (4.23), то сумеем начертить и линии поля и эквипотенциалы. Фиг. 4.13 демонстрирует этот результат. Но сперва пришлось решить задачу аналитически!
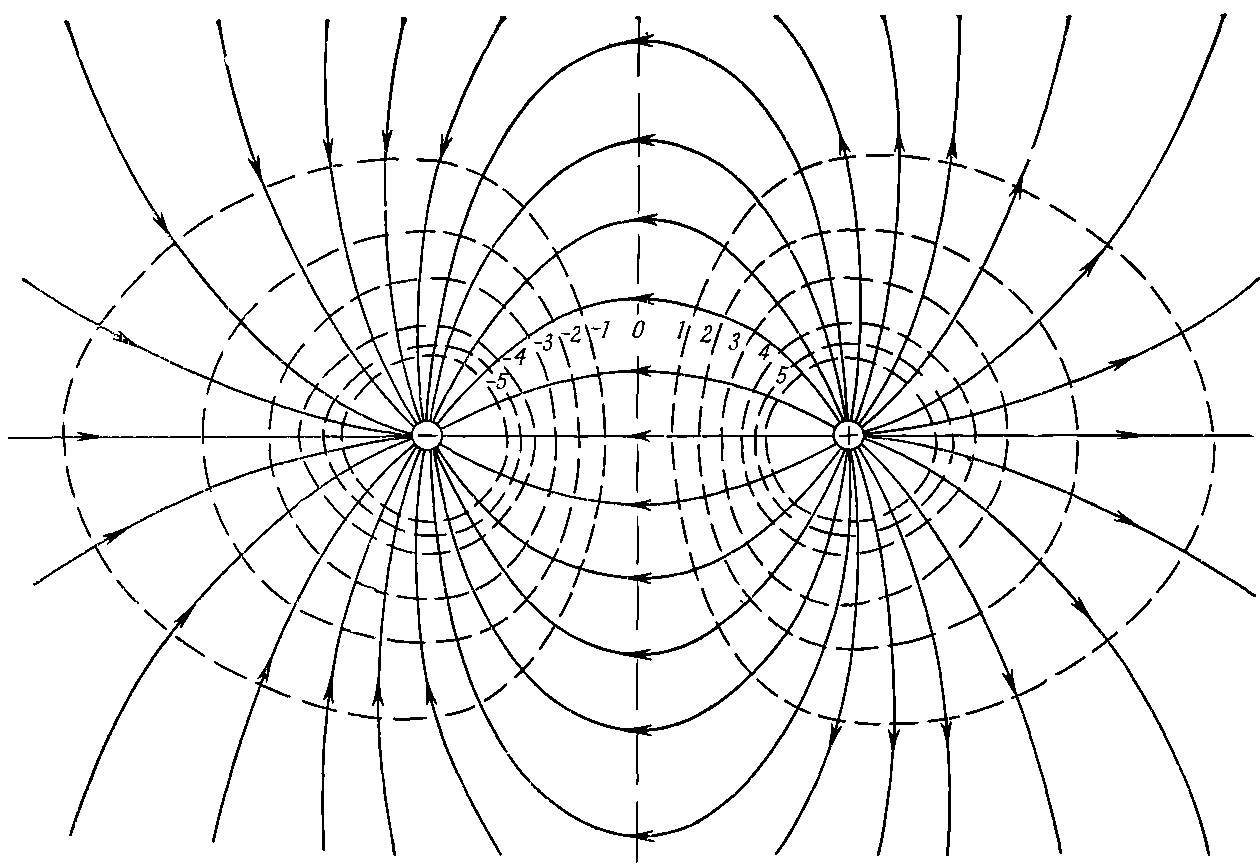
Фиг. 4.13. Линии поля и эквипотенциальные поверхности для двух равных, но »разноименных точечных зарядов.