§ 3. Граничная частота

Уравнение (24.16) для k_z на самом деле имеет два корня — один с плюсом, другой с минусом. Ответ следует писать так:

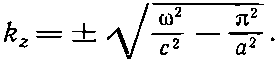(24.20)

Смысл этих двух знаков просто в том, что волны в волноводе могут бежать и с отрицательной фазовой скоростью (в направлении —z), и с положительной. Волны, естественно, должны иметь возможность бежать в любую сторону. И раз одновременно могут существовать оба типа волн, то решение в виде стоячих волн тоже возможно.

Наше уравнение для k_z сообщает нам также, что высшие частоты приводят к большим значениям k_z, т. е. к более коротким волнам, пока в пределе больших ? величина k не станет равной ?/с — тому значению, которое бывает, когда волна бежит в пустоте. Свет, который мы «видим» сквозь трубу, все еще бежит со скоростью с. Но посмотрите зато, какая странная вещь получается, когда частота убывает. Сперва волны становятся все длиннее и длиннее. Но если частота ? станет чересчур малой, то под корнем в (24.20) внезапно появится отрицательное число. Это произойдет, когда ? перевалит через ?с/а или когда ?₀ станет больше 2а. Иначе говоря, когда частота становится меньше некоторой критической частоты ?_c=?с/а, волновое число k_z (а также ?_g) становится мнимым и никакого решения у нас не остается. Или остается? Кто, собственно, сказал, что k_z должно быть действительным? Что случится, если оно станет мнимым? Уравнения-то поля по-прежнему ведь будут удовлетворяться. Может быть, и мнимые k_z тоже представляют какую-то волну?

Предположим, что ? действительно меньше ?_c; тогда можно написать

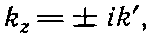(24.21)

где k' — действительное положительное число

(24.22)

Если теперь вернуться к нашей формуле (24.12) для Е_y, то надо будет написать

(24.23)

что можно также представить в виде

(24.24)

Это выражение приводит к полю Е, которое во времени колеблется как e^i?t, а по z меняется как e^±k'z. Оно плавно убывает или возрастает с z, как всякая действительная экспонента. В нашем выводе мы не думали о том, откуда взялись волны, где их источник, но, конечно, где-то в волноводе он должен быть. И знак, который стоит при k', должен быть таков, чтобы поле убывало при удалении от источника волн.

Итак, при частотах ниже ?_с=?с/а волны вдоль трубы не распространяются; осциллирующее поле проникает в трубу лишь на расстояние порядка 1/k'. По этой причине частоту ?_с называют «граничной частотой» волновода. Глядя на (24.22), мы видим, что для частот чуть пониже ?_c число k' мало, и поля могут проникать в трубу довольно далеко. Но если ? намного меньше ?_с, коэффициент k' в экспоненте равняется ?/а, и поле отмирает чрезвычайно быстро (фиг. 24.7). Поле убывает в е раз на расстоянии а/?, т. е. на трети ширины волновода. Поля проникают в волновод на очень малое расстояние от источника.

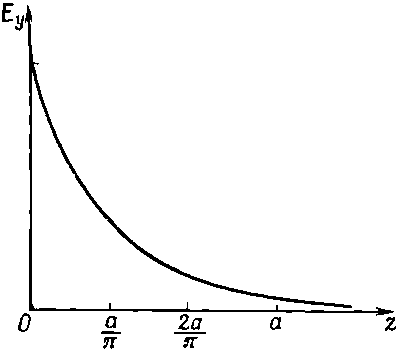
Фиг. 24.7. Изменение Е_y с ростом z при ???_c.

Мы хотим еще раз подчеркнуть эту характерную черту нашего анализа прохождения волн по трубе — появление мнимого волнового числа k_z. Когда, решая уравнение в физике, мы получаем мнимое число, то это обычно ничего физического не означает. Для волн, однако, мнимое волновое число действительно нечто означает. Волновое уравнение по-прежнему удовлетворяется; оно только означает, что решение приводит к экспоненциально убывающему полю вместо распространяющихся волн. Итак, если в любой задаче на волны k при какой-то частоте становится мнимым, это означает, что форма волны меняется — синусоида переходит в экспоненту.