§ 2. Уравнения Максвелла в диэлектрике
Наличие в веществе поляризации означает, что там возникают поляризационные заряды и токи, которые необходимо учитывать в полных уравнениях Максвелла при нахождении полей. Сейчас мы собираемся решать уравнения Максвелла для случая, когда заряды и токи не равны нулю, но неявно определяются вектором поляризации. Нашим первым шагом должно быть явное нахождение плотности зарядов ? и плотности тока j, усредненных по тому же самому малому объему, который имелся в виду при определении вектора Р. Потом необходимые нам значения ? и j могут быть определены из поляризации. В гл. 10 (вып. 5) мы видели, что когда поляризация Р меняется от точки к точке, то возникает плотность зарядов:
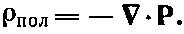 (32.9)
(32.9)
В то время мы имели дело со статическими полями, но эта же формула справедлива и для переменных полей. Но когда Р изменяется со временем, заряды движутся, так что появляется поляризационный ток. Каждый из осциллирующих зарядов вносит в ток свой вклад, равный произведению его заряда qe на скорость v. Когда же таких зарядов в единице объема N штук, то они создают плотность тока j:
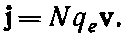
Ну а поскольку известно, что v=dx/dt, то j=Nqedx/dt, что как раз равно dP/dt. Следовательно, при переменной поляризации возникает плотность тока
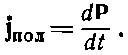 (32.10)
(32.10)
Наша задача стала теперь простой и понятной. Мы пишем уравнения Максвелла с плотностями заряда и тока, определяемыми поляризацией Р посредством уравнений (32.9) и (32.10). (Предполагается, что других зарядов и токов в веществе нет.) Затем мы свяжем Р с Е формулой (32.5) и будем разрешать их относительно Е и В, отыскивая при этом волновое решение.
Но прежде чем приступить к решению, мне бы хотелось сделать одно замечание исторического характера. Первоначально Максвелл писал свои уравнения в форме, отличающейся от той, в которой они используются нами. И именно потому, что уравнения писались в другой форме в течение многих лет (да и сейчас многими пишутся так), я постараюсь объяснить вам разницу. В те дни механизм диэлектрической проницаемости не был понятен с ясностью и полнотой. Не была ясна ни природа атомов, ни существование поляризации в веществе. Поэтому тогда не понимали, что ?·P дает дополнительный вклад в плотность заряда ?. Были известны только заряды, не связанные в атомах (такие, как заряды, текущие по проводу или возникающие при трении).
Сегодня же мы предпочитаем обозначать через ? полную плотность зарядов, включая в нее и заряды, связанные с индивидуальными атомами. Если назвать эту часть зарядов ?пол, то можно написать

где ?др— плотность зарядов, учтенная Максвеллом и относящаяся к другим зарядам, не связанным с определенными атомами. При этом мы бы написали
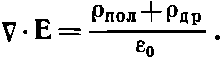
После подстановки ?пол из (32.9) получаем
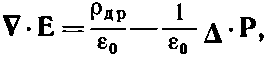
или
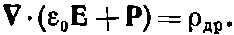 (32.11)
(32.11)
В плотность тока, фигурирующую в уравнениях Максвелла для ??B, вообще говоря, тоже вносится вклад от связанных атомных электронных токов. Поэтому мы можем написать
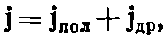
причем уравнение Максвелла приобретает вид
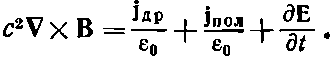 (32.12)
(32.12)
Используя уравнение (32.10), получаем
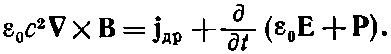 (32.13)
(32.13)
Теперь вы видите, что если бы мы определили новый вектор D
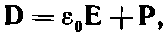 (32.14)
(32.14)
то два уравнения поля приняли бы вид
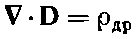 (32.15)
(32.15)
и
 (32.16)
(32.16)
Это и есть та форма уравнений, которую использовал Максвелл для диэлектриков. А вот и остальные два уравнения:

и
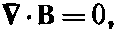
которые в точности совпадают с нашими.
Перед Максвеллом и другими учеными того времени вставала проблема магнетиков (за них мы вскоре примемся). Они ничего не знали о циркулирующих токах, ответственных за атомный магнетизм и поэтому, в плотности тока утеряли еще одну часть. Вместо уравнения (32.16) они на самом деле писали
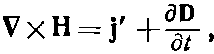 (32.17)
(32.17)
где Н отличается от ?0с2В, так как последнее учитывает эффекты атомных токов. (При этом j' представляет то, что осталось от токов.) Таким образом, у Максвелла было четыре полевых вектора: Е, D, В и Н, причем в D и Н скрывалось то, на что он не обратил внимания, — процессы, происходящие внутри вещества. Уравнения, написанные в таком виде, вы встретите во многих местах.
Чтобы решить их, необходимо как-то связать D и Н с другими полями, поэтому зачастую писали
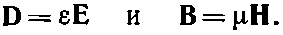 (32.18)
(32.18)
Однако эти связи верны лишь приближенно для некоторых веществ, и то лишь когда поля не изменяются слишком быстро со временем. (Для синусоидально изменяющихся полей зачастую можно писать уравнения таким способом, считая при этом ? и ? комплексными функциями частоты, но для произвольных изменений поля со временем это неверно.) На какие только ухищрения не пускаются ученые, чтобы решить уравнения! А мне кажется, что правильнее всего оставить уравнения записанными через фундаментальные величины, как мы понимаем их теперь, т. е. как раз то, что мы и проделали.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК