§ 1. Векторный потенциал
В этой главе мы продолжим разговор о магнитостатике, т. е. о постоянных магнитных полях и постоянных токах. Магнитное поле и электрические токи связаны нашими основными уравнениями:
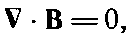(14.1)
и
(14.2)
На этот раз нам нужно решить эти уравнения математически самым общим образом, а не ссылаться на какую-нибудь особую симметрию или на интуицию. В электростатике мы нашли прямой способ вычисления поля, когда известны положения всех электрических зарядов: скалярный потенциал ? дается просто интегралом по зарядам, как в уравнении (4.25) на стр. 77. Если затем нужно знать электрическое поле, то его получают дифференцированием ?. Мы покажем сейчас, что для нахождения поля В существует аналогичная процедура, если известна плотность тока j всех движущихся зарядов.
В электростатике, как мы видели (из-за того, что rot от Е везде равен нулю), всегда можно представить Е в виде градиента от скалярного поля ?. А вот rot от В не везде равен нулю, поэтому представить его в виде градиента, вообще говоря, невозможно. Однако дивергенция В везде равна нулю, а это значит, что мы можем представить В в виде ротора от другого векторного поля. Ибо, как мы видели в гл. 2, § 8, дивергенция ротора всегда равна нулю. Следовательно, мы всегда можем выразить В через поле, которое мы обозначим А:
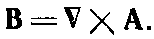(14.3)
Или, расписывая компоненты:
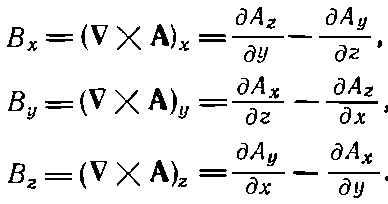(14.4)
Запись B=??A гарантирует выполнение (14.1), потому что обязательно
Поле А называется векторным потенциалом.
Вспомним, что скалярный потенциал ? оказывается не полностью определенным. Если мы нашли для некоторой задачи потенциал ?, то всегда можно найти столь же хороший другой потенциал ?', добавив постоянную:
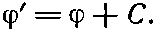
Новый потенциал ?' дает те же электрические поля, потому что градиент ?С есть нуль; ?' и ? отвечают одной и той же картине.
Точно так же у нас может быть несколько векторных потенциалов А, приводящих к одним и тем же магнитным полям. Опять-таки, поскольку В получается из А дифференцированием, то прибавление к А константы не меняет физики дела. Но для А свобода больше. Мы можем добавить к А любое поле, которое есть градиент от некоторого скалярного поля, не меняя при этом физики. Это можно показать следующим образом. Пусть у нас есть А, которое в какой-то реальной задаче дает правильное поле В. Спрашивается, при каких условиях другой векторный потенциал А', будучи подставлен в (14.3), дает то же самое поле В. Значит, А и А' имеют одинаковый ротор
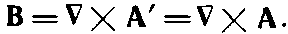
Поэтому
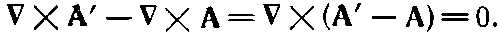
Но если ротор вектора есть нуль, то вектор должен быть градиентом некоторого скалярного поля, скажем ?, так что А'-A=??. Это означает, что если А есть векторный потенциал, отвечающий данной задаче, то при любом ?
(14.5)
также будет векторным потенциалом, в одинаковой степени удовлетворяющим данной задаче и приводящим к тому же полю В.
Обычно бывает удобно уменьшить «свободу» А, накладывая на него произвольно некоторое другое условие (почти таким же образом мы считали удобным — довольно часто — выбирать потенциал ? равным нулю на больших расстояниях). Мы можем, например, ограничить А, наложив на него такое условие, чтобы дивергенция А чему-нибудь равнялась. Мы всегда можем это сделать, не задевая В. Так получается потому, что, хотя А' и А имеют одинаковый ротор и дают одно и то же В, они вовсе не обязаны иметь одинаковую дивергенцию. В самом деле, ?·A'=?·A+?2?, и, подбирая соответствующее ?, можно придать ?·A' любое значение.
Чему следует приравнять ?·А? Выбор должен обеспечить наибольшее математическое удобство и зависит от нашей задачи. Для магнитостатики мы сделаем простой выбор
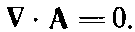(14.6)
(Потом, когда мы перейдем к электродинамике, мы изменим наш выбор.) Итак, наше полное определение[17] А в данный момент есть ??A=B и ?·А=0.
Чтобы привыкнуть к векторному потенциалу, посмотрим сначала, чему он равен для однородного магнитного поля В0. Выбирая ось z в направлении В0, мы должны иметь
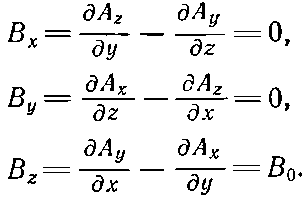(14.7)
Рассматривая эти уравнения, мы видим, что одно из возможных решений есть
Или с тем же успехом можно взять
Еще одно решение есть комбинация первых двух
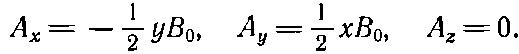(14.8)
Ясно, что для каждого поля В векторный потенциал А не единственный; существует много возможностей.
Третье решение [уравнение (14.8)] обладает рядом интересных свойств. Поскольку x-компонента пропорциональна -y, а y-компонента пропорциональна +x, то вектор A должен быть перпендикулярен вектору, проведенному от оси z, который мы обозначим r' (штрих означает, что это не вектор расстояния от начала). Кроме того, величина А пропорциональна ?(x2+y2) и, следовательно, пропорциональна r'. Поэтому А (для однородного поля) может быть записано просто
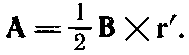(14.9)
Векторный потенциал А равен по величине Br'/2, и вращается вокруг оси z, как показано на фиг. 14.1.
Фиг. 14.1. Однородное магнитное поле В, направленное по оси z, соответствует векторному потенциалу А (А=Вr'/2), который вращается вокруг оси z. т' — расстояние до оси z.
Если, например, поле В есть поле внутри соленоида вдоль его оси, то векторный потенциал циркулирует точно таким же образом, как и токи в соленоиде.
Векторный потенциал однородного поля может быть получен и другим способом. Циркуляция А вдоль любой замкнутой петли ? может быть выражена через поверхностный интеграл от ??A с помощью теоремы Стокса [уравнение (3.38), стр. 63]
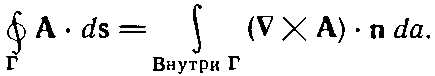(14.10)
Но интеграл справа равен потоку В сквозь петлю, поэтому
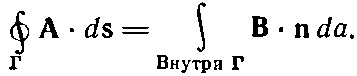(14.11)
Итак, циркуляция А вдоль всякой петли равна потоку В сквозь петлю. Если мы возьмем круглую петлю радиуса r' в плоскости, перпендикулярной однородному полю В, то поток будет в точности равен
Если выбрать начало отсчета в центре петли, так что А можно считать направленным по касательной и функцией только от r', то циркуляция будет равна
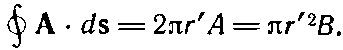
Как и раньше, получаем
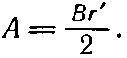
В только что разобранном примере мы вычисляем векторный потенциал из магнитного поля, обычно поступают наоборот. В сложных задачах всегда проще найти векторный потенциал, а затем уже из него найти магнитное поле. Сейчас мы покажем, как это можно сделать.